Прогрессивная математика

Начало

ЧАСТЬ 4

НЕПРЕРЫВНЫЙ ПРОЦЕСС МАТЕМАТИКИ

Пообщавшись с учеными людьми, записавшись на подготовительные курсы одного из ведущих вузов страны, я пришел к выводу о пользе такого своего действа, когда узнал много нового. Естественно, что всего человек знать не может и мы пользуемся уже сложившейся информацией не имея представления о непрерывности процесса в лоне отдельной науки математики.

Этот процесс безусловно имеет какую-то свою собственно выраженную  историю в  общей системе мировой философии. Эта тема достаточно интересная, но  советовать, что-либо людям ученым, как то не комфортно, и придется самому эту тему оформить, для упорядочения своего собственного мировоззрения. И начать придется с пальцевого счета.

Можно понять почему именно  с пальцев, зная что этот естественный инструмент для счета человек имеет всегда и в бытовых ситуациях до сих пор демонстрирует на пальцах нужные числа.

Уже говорилось о том, что параллельно с языковыми различиями древних стран существовал секретный язык древних строителей (архитекторов), с помощью которого они могли общаться между собой.  До нашего времени  сохранился только трактат римского архитектора Витрувия (80 г. до н.э.), который использовал в своей работе известный художник Леонардо да Винчи.

Итак, один из "акцентов" языка философов мы определили и "Витрувианский человек" демонстрирует утверждение Протагора (ок. 490-ок.420 до н.э.), что человек есть мера всех вещей. Вот от этого утверждения и будем отталкиваться не вникая в какие-либо утверждения кто и когда чего-то открыл или изобрел. Когда и сейчас ни чего доказать невозможно, зная о том, что и на начало эпохи "Нового Завета" существовала иероглифическая письменность.

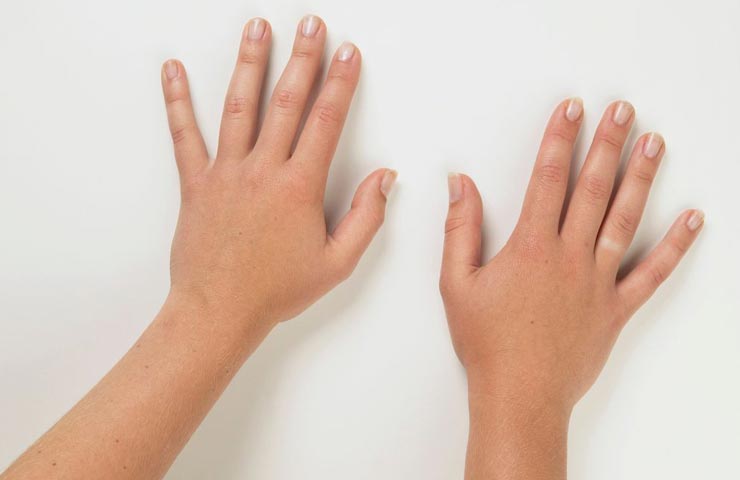
Итак, рука человека демонстрирует первый счетный инструмент, в котором четыре пальца являются первичной системой счета, в которой весь числовой ряд представляет 1, 2, 3, 4. Сумма же чисел, образующих этот ряд, равен десяти (1+2+3+4=10). Другим важным вопросом является история тригонометрии, которую по мнению историков создали астрономы использующие вавилонскую систему чисел.

Спорить с этим не будем,  но в "попугаях" вычислять углы не возможно. Здесь все сводится к тому, что греки получили эту систему во  II веке до н. э., когда как мы знаем что финикийские корабли  к этому времени давно уже  бороздили просторы океанов. Правда в основном это было каботажное плавание, но это не суть важно, когда первые древнегреческие философы, сведения о которых дошли до нас, жили в VI веке до нашей эры.

Это Фалес и Пифагор. Итак рука, это инструмент для счета, приложим к этому инструменту вторую руку, еще четыре пальца увеличив тем самым числовой ряд, в котором среднюю позицию занимают сдвоенные большие пальцы.  Которые являются средней точкой числового ряда  цифра 5, где равно удаленные от этого центра цифры в сумме составляют число 10: 4+6=10; 3+7=10; 2+8=10; 1+9=10.

Считается, что римские цифры существуют с V века до нашей эры и какую именно цифирь использовал Пифагор составляя свою таблицу, мы не знаем, но тот факт, что за пятьсот лет до н.э. существует римская система счисления не оспорим. Это не клинопись и не иероглифы. И тогда со спокойной совестью остаемся в числовой системе, какой бы она не была.

Здесь надо сказать, что изначально таблица Пифагора имела девятиуровневый, девятизначный числовой ряд состоящий из 81 числа. По этой таблице и работали все античные философы вычисляя свои задачи, самая известная из которых вычисление квадратуры круга имеющая прямые отношения к знаменитой теореме Пифагора.  Которая наглядно представлена как ряд  прямых квадратов чисел 3, 4, 5 == 9, 16, 25.

Где последний квадрат 25 является центром таблицы Пифагора. Здесь формула приближения Пи  предположительно составляла как √9 = 3, о чем мы можем увидеть в книге Аль-Бируни. Это очень важная информация, которую нужно помнить.

Этот же персидский мыслитель сообщает, что в последствии астрономы использовали в своих расчетах приближение Пи √10 ≈ 3.16, которое надо полагать, появляется с применением десятичной системы счисления.  Появление которой можно связать как с римскими цифрами, так и с евклидовом пространством (Евклид жил в III веке до н.э.), точку в котором можно представить  как упорядоченную пару  (x; y) действительных чисел.

Десятеричная система счисления потребовалась с развитием кораблестроения, когда первым критиком навигации оказался мифический Одиссей, заблудившийся на обратном пути из Трои. Свой вклад в историю кораблевождения внес Фемистокл (524 до н.э. – 459 до н.э.) афинский флотоводец. Есть пример, когда  историк Геродот жестоко высмеивал  финикийцев: " И говорят, по-моему, неправду, а другой кто-нибудь, может быть, поверит, что, плывя вокруг Ливии, они имели солнце справа».

Это кажущееся противоречие потребовало более точных расчетов навигации, когда

мы видим у астронома Аль-Хорезми, который ссылается на трактат Ариабаты, который вычисляет Пи = 3,1416, хотя сам применяет более привычное древним философам √10 ≈ 3.16. Сказав (по слухам), что только бог знает, что вычисляет Ариабата:

"Прибавьте четыре к сотне, затем умножьте результат на восемь и прибавьте шестьдесят две тысячи. ((4 + 100) х 8 + 62000)/20000 = 62832/20000 = 3,1416)".

62832/20000 = 3,1416

Здесь мы видим ряд прямых квадратов 10²=100; 100²=10000

Левая часть выражения показывает на число 62832, а правая на число 31416, которое в два раза меньше левого числа. Здесь мы видим, как количество нулей в знаменателе  влияет на место запятой числа "Пи". И выводится аксиома: Пи равно половине окружности при радиусе равном единице.

О культурном заражении  уже говорилось ранее, поэтому про Математический папирус Ахмеса,  Московский математический папирус, и другие артефакты не упоминаются. Когда у нас есть прямая последовательность от греческой школы математики  сохраняющаяся на востоке и проявленная в трудах Ариабаты, где приводятся правила суммирования натуральных квадратов и кубов, некоторых других рядов.

Позиция Ариабаты сходится с взглядами локаятиков – последователей философской школы древнеиндийских материалистов. Тут расхождение взглядов Ариабаты с другими астрономами основано на религиозных воззрениях.

Отметив в работах Аль-Хорезми и Аль-Бируни состояние математического процесса от середины к концу первого тысячелетия (от Р.Х.). Мы видим далее, что  все объявленные результаты исследований показавших универсальность числа Пи датированы XVII-XVIII веками, когда эстафета переходит от арабских мыслителей назад к европейской философии. И покажем прямую преемственность пифагорейских традиций.

Здесь математик Леонард Эйлер (1707 - 1783 гг.) участвующий в марафоне решения задачи квадратуры круга, как и многие философы саму задачу не решил, но придумал, что-то другое. По сути повторяя "фокус" Ариабаты он вычислил ряд обратных квадратов: 1/1² + 1/2² + 1/3² + 1/4² + 1/5² +..... Эти вычисления о бесконечно малых величинах Эйлер завершил суммой Пи²/6 или ≈ 1,644934.

И как водится этот вывод Эйлера прошел бесконечное уточнение, включающее вычисления на компьютере, до миллионной цифры после запятой. Количество написанных по этому поводу диссертаций не ведомо, но они безусловно есть. Почему мы ассоциируем Эйлера с Ариабатой? По той причине, что все вычисления до миллионной цифры значения Пи, а также суммы ряда обратных квадратов бесполезно и ни на что не влияет.

Мы запоминали ранее важное значение вычислений основанных на приближение Пи √9 = 3. Когда вся формула выглядит так 6/2 = 3. И здесь поставив значение Пи = 3 в полученную Эйлером сумму мы имеем следующее значение 3²/6 = 1,5 без какого либо миллионного хвоста не нужной цифири. Подкрепленной вавилонской системой счисления, ни кому не известной, но существующей. Но это уже другая история, которая связана с мистикой о энергетических процессах.

Маленькое рассуждение о вавилонской системе, которая базируется на √9 = 3. Здесь формула отношения диаметра круга к окружности будет 6/2 = 3. Когда деление круга на 6 частей-углов по 60°, позволяет говорить о шестидесятеричной системе счета, хотя как уже было сказано это не так. Говоря об энергиях прямых и обратных квадратов, в первом случае будет 1, а во втором 1,5, что говорит о разных потенциалах.

МАГИЯ ЧИСЕЛ

1 , 4 , 9 , 16 , 25 , 36 , 49 , 64 , 81 , 100 , 121 , 144 , 169 , 196…..
3 , 5 , 7 , 9 , 11 , 13 , 15 , 17 , 19 , 21 , 23 , 25 , 27 ……

И наконец:
Знак божественной триады 999=27=9
Число Дьявола 666=18=9

 1+2+3+4+…+35+36 = 666.

Делим это число наискось: 234 + 432 = 666, так называемое число зверя, при этом 6×6×6 = 216, полученную числовую величину множим на 2 и получаем = 216 × 2 = 432.
Два зеркальных числа 432 + 234 дают в сумме 666.

И последний, совершенно не нужный расчет. Размышляя логически, можно поставить такой вопрос: Если девятка и четверка отображает человека, то (девятка с тройкой – означает животное), что же будет означать девятка с пятеркой? Сейчас же и посмотрим: 9×5 = 45, в принципе получился тот же человек = 1+2+3+4+…+44+45 = 999, но «божественный», представленный в трех ипостасях Божественной Триады.

Не получилось? В этом и вся хитрость. Уберите дьявольское начало (36), из полученной суммы и будет то, что надо. Дьявольским началом мы назвали эту цифровую составляющую потому, что 666 талантов золота получал царь Соломон каждый год.

Изображения взяты в интернете.