Прогрессивная математика

ПРОГРЕССИВНАЯ МАТЕМАТИКА

О том, что математика это язык бога, а наука это тоже религия я писал лет двадцать назад в одной из своих работ. А сейчас то же самое услышал из уст ученого математика. Стало быть в этой сфере научного познания мира произошел очередной переход на более качественное мышление, когда виртуальный мир математики, математическое мышление или прогрессивная математика, аналогична религиозному восприятию мира.

Энциклопедия Кольера, говорит о том, что прогрессия это последовательность чисел, получаемых по некоторому правилу, например, возрастанию путем прибавления некоего числа. Суть в том, что сумма n членов равна числу членов, умноженному на полу сумму первого и последнего членов. Например, сумма последовательных целых чисел от 1 до 50 равна (1/2)*50*51 = 1275. Множество чисел иногда называется гармонической прогрессией, если величины, обратные этим числам, являются членами арифметической прогрессии.

Например, числа 1, 1/2, 1/3, 1/4,... при n, стремящемся к бесконечности, стремится к некоторому пределу, который называется постоянной Эйлера. Говоря о прогрессиях надо упомянуть Архимеда умеющего  вычислять сумму числа членов геометрической прогрессии, которому приписывается вычисление числа "пи". Архимед не смог решить "Античные задачи", и вычислил нужное число механически, сделав при этом несколько изобретений, например, пружину.

Имея свою "Архимедову ванну" Архимед мысля логически мог бы решить и задачу о кубе, подогнав нужную грань и окунуть его в свою ванну для проверки. Но не случилось. Тесать гранит, подгоняя нужные размеры тяжелая работа, и здесь конечно лучше решить задачу вычислив размеры куба. Мы эту задачу решали двадцать лет, а у античных философов не было ни времени, ни опыта решения подобных задач.

О боге говорит математик Алексей Савватеев - доктор физико-математических наук и кандидат экономических наук, профессор и научный сотрудник, который активно занимается популяризацией математики. В СМИ вышло интервью с Савватеевым, где он говорит  о своих религиозных взглядах и взаимосвязи науки и религии, напоминая что до 1917 года это было абсолютно гармонично.

Случай с Лапласом, якобы говорившего Наполеону о том, что не нуждается в концепции бога, здесь даже не исключение, потому что "демон" Лапласа относится к той же реальности, что и бог. И в то же время полагаю, что не нужно считать ученых (теорема Геделя) доказавшими существования Бога. К богу эти ученые не приблизятся, а учеными быть перестанут, превратившись в обыкновенных шарлатанов, когда научное звание в религии преференций не дает.

Хотя религия и математика - это две ипостаси нашего мира, и каждая из них чрезвычайно глубока. Но в каждой отрасли есть свои краснодеревщики, которые в дела других мастеров не лезут.  Если хочешь общаться с богом, надо идти к попу, для которого посредничество между всевышним и человеком является повседневной работой, в которой инсайт не предусмотрен.

Почему именно Савватеев привлекает внимание? Своим поведением, человека не от мира сего, который мог бы претендовать на такие аналоги, как личность Пифагора или циркового артиста. Здесь нет ничего зазорного, когда со времен античного мира именно в цирке представлялись непонятные и удивительные вещи, например "петля Мебиуса", которую Мебиус увидел в цирке. Говорят, что и Агриппа считал физиков фокусниками

До сего времени в развлекательных ток шоу, выступают люди показывающие необычные способности, после объявления номера выступления какого-либо профессора алхимии. Кто то рисует сразу двумя руками, кто то демонстрирует свою интуицию, память или поет в диапазоне 2-3 октавы, на разные голоса.

Сравнивая математическую науку с религией математик, имеет ввиду глубину знаний посвященного в эти дисциплины человека, когда одна из них несет веру, а другая знания.

Когда человек для того, чтобы понять о чем идет речь, должен вникнуть в суть прочитав соответствующую литературу. Здесь математик солидарен с Теософией - религиозно-философским учением созданным Е.П.Блаватской, состоящее в мистическом бого-познании, о возможности непосредственного постижения Бога с помощью мистического откровения и интуиции, доступных избранному кругу лиц. Как бы современные атеисты ученые не выпячивали грудь от самооценки, а Тайную Доктрину они не расшифровали за небольшим исключением.

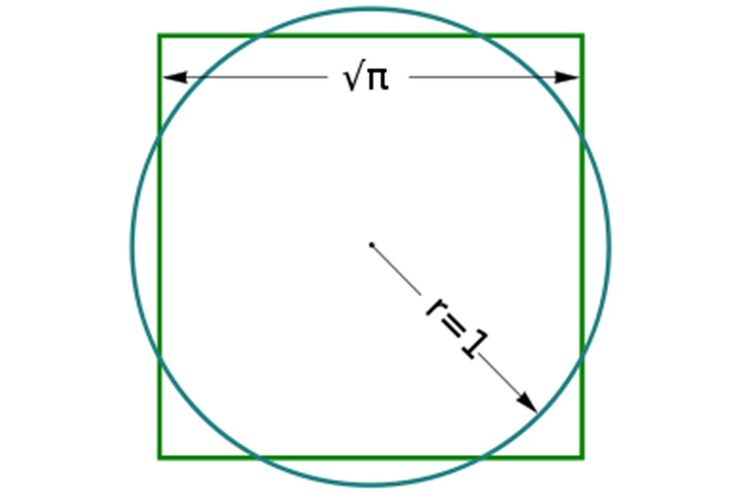
Рассказывая о математике Алексей Саватеев демонстрирует новый тип мышления, когда подобно Архимеду он за несколько минут вычисляет константу "Пи", говоря о том, что ее в определенном случае можно принять за единицу. И на вопрос: "Почему число Пи трансцендентно? Говорит о том, что доказывать это надо в течении семи лекций".

Надо признать, что "древние" в этом случае были мудрее, придумав задачи, в которых построение нужной фигуры, происходит всего за несколько минут. Наш алгоритм позволяет это сделать, хотя для решения "античных задач" нам пришлось потратить от десяти до двадцати лет. Савватеев античных задач не решил, обойдя требования использования для решения задач только двух инструментов, линейки и циркуля.

И здесь я с ним не согласен, надо быть честным по отношению к предшественникам, которые отнюдь не были идиотами, когда считали своим долгом отметиться в этой затянувшейся олимпиаде. А если разобраться с этим вопросом конкретнее, то академики поступили странным образом, когда переиначили и по сути дела "испортили" древние задачи, внеся туда дополнительные инструменты, которых в условиях задач нет.

А потом не смогли решить древние задачи и признали античные задачи не решаемыми, по сути своей пренебрежительно, на мой взгляд, отнеслись к древнегреческим философам, решения которых мы знаем.  Пытаясь решить античные задачи Платон применял сравнительную аналогию, Гиппократ предложил свои "Луночки", другие пытались применить строительство многоугольников и т.д.

Да и говорили, что одну из этих задач решил норвежский математик Нильс Абель (1802-1829), который вскоре умер и французская академия признавшая "античные задачи" нерешаемыми не стала обращать на это внимание. Скорее всего Абель так же подогнал решение к нужному ответу, как это делают современные математики, по семь часов гоняя цифирь в разные стороны, чтобы получить необходимый результат. И в этом религия и математика идут параллельно с глубокой древности.

Понятия виртуальности и реальности изучаются философской онтологией и гносеологией, а также социальной философией, при этом понятие реальности рассматривается через бытие в его сопоставлении с небытием, а также возможными формами бытия. Которое возникает при решении "некорректных задач". Так один из кандидатов физмат наук высказался с экрана телевизора о том, что задачу Пуанкаре, которую решил Григорий Перельман во всем мире могут понять только десяток человек.

Подразумевая то, что существуют высшие сферы науки для избранных. Об этом же говорит и математик Савватеев. Бесполезно вступать в полемику с доктором физико-математических наук, который с помощью своего извращенного разума способен постигать разные "виртуальности" сознания. Однако надо подкрепить его сомнение, что египтяне вряд ли могли вычислить квадратуру круга используя такие меры как локоть, в расчётах материального мира Вселенной, как основной объект изучения естественных наук.

Вычисляя число "Пи" Савватеев говорит, что он не знает почему египтяне применили здесь 1/9, но такая пропорция дает возможность вычисления отношения "Пи".

Однако египтяне не вычисляли квадратуры круга ни в локтях, ни в "попугаях" (иероглифах), эти сведения дает Елена Блаватская в своей космогонии (Тайная Доктрина), ссылаясь при этом на Пифагора, а не на египтян. Египтяне исходили из какой-то условной единицы измерения, например "локоть" значения которого сильно отличались не только в годы разных династий, а даже в эпоху одной династии.

Приведем несколько примеров разницы в длине локтя. Локоть состоял из семи ладоней, а ладонь – из четырех пальцев. Все размеры, приводимые египтянами в своих записях, указаны в локтях, ладонях и пальцах. Для измерения расстояний на местности использовали веревку, на которой длина локтя была отмечена узлами. С какой точностью производились измерения покажем на примере пирамиды стороны основания которой имеют следующую длину:

Северная 9065,1 дюйма

Восточная 9070,5 дюйма

Южная 9073,0 дюйма

Западная 9069,2 дюйма

В среднем: 9069,45 дюйма

Из этих подсчетов хорошо видно, что разница между самой длинной и самой короткой стороной составляет 7,9 дюйма, которая объясняется гораздо проще, чем результат предыдущих измерений. На вопрос, можно ли получить такую точность с помощью измерительной веревки, ответить, не проведя эксперимент лично, нельзя.

Текст египетских канонов не сохранился, а есть только ссылка на трактат «Предписание для стенной живописи и канон пропорций».

Где по разным источникам первый канон слагает рост человека из 6 ступней ноги, второй разбивает каждую ступню еще на три части и таким образом составляет рост человека из 18 единиц, третий канон складывает рост человека из 21 части с четвертью. Все это так, но термин о том, что "Человек мера всех вещей" мы знаем от Протагора (ок. 490-ок.420 до н.э.). У человека просматриваются те же аналогии: -пуп человека – делит тело человека в золотом сечении.

Возьмите линейку и измерьте длину трех фаланг среднего пальца и пясти. Поделив эти числа на длину первой фаланги, вы с поразительной точностью обнаружите 4 члена ряда золотого сечения: 1, Ф=1,618, Ф²=2,618 , Ф³=4,234. Пифагореец Поликлет показал, что золотая пропорция присуща не только абстрактной геометрической фигуре, главному пифагорейскому символу – пятиконечной звезде, но и естественным образом входит в пропорции человека.

Анализ пропорций «Дорифора» и других скульптур Поликлета подтверждает предположения: в скульптурах Поликлета с большой точностью выдержаны пропорции ряда золотого сечения. 1, φ¹,φ²,φ³,φ,φ,φ.

1,1,2,3,5,8,13,21,34,55,89,144,233,377,…,Эта последовательность была описана в 1202 г. в «Книге об абаке» итальянским купцом и математиком Леонардо из Пизы, известным более по его прозвищу – Фибоначчи.

Ряд золотого сечения и тесно связанный с ним ряд Фибоначчи обладают массой исключительных математических свойств, например, числовой ряд 113355, который вычислял математик Савватеев сделав из него пропорцию. Сказав при этом: "Я не знаю откуда появился этот ряд, но я опираясь на него, могу делать определенные вычисления". Вот это его заявление говорит о том, что математика перешла на другой уровень развития, когда используя опорные точки математики могут решать поставленные задачи без дополнительных инструментов.

Здесь нет, каких-либо  критических замечаний, а наоборот приветствуется манера поведения учителя математики, который может отбросить в сторону все числительные системы измеряемые в "локтях" или "попугаях". Забыв все спекулятивные двенадцатеричные, и иные числовые системы индейцев майя, когда даже история не сохранила ни имена спекулянтов продвигающих эти системы, ни каких-либо расчётов по ним.

Итак, какие расчётные системы и достижения мы имеем на сегодняшний день:

Около ста лет назад академик Вернадский писал, что "античные задачи" с заявленными инструментами линейка и циркуль не имеют решения. Мы эти задачи решили именно так, как того требуют условия задачи, - с помощью линейки и циркуля. Около ста лет назад Елена Блаватская опубликовала свою космогонию "Тайная Доктрина", с которой согласились все эзотерические школы.

Считается, что Ариабата изобрёл понятие "нуля", нашел точное значение числа "Пи" (62832/20000 = 3.1416) и ввел в тригонометрию функцию (1 - cos x). Когда, за единицу измерения линий синуса, косинуса и синуса-верзуса принималась дуговая минута. Таблица синусов составлена через каждые 3°45′=225′, т.е. через 1/24 часть дуги квадранта. Для составления этой таблицы необходимо знать 5 значений синуса, а именно: синус 18°, синус 30°, синус 36°, синус 45°, синус 60°. Значения этих величин легко получить, используя радиусы правильных многоугольников, имея при этом в виду, что sina=Rsina.

При этом Пифагор жил в VI- V вв. до н.э. Ариабата же родился в– 476 г. н.э. т.е. на тысячу лет позже времени в котором жил Пифагор. В то же время, знания греческой, вавилонской и египетской школ философии могли попасть в Индию и с войсками Александра Македонского. Ученые относят десятичную систему счисления к III тыс. до н.э. и в это же время нельзя утверждать, что найденные знаки являются именно десятеричной системой счисления.

Рассмотрим вычисления числа "Пи". И здесь вычисления Ариабаты ни чем не подтверждены, в то время когда мы знаем, что число "Пи" вычислял Архимед живший ранее Ариабаты почти на шестьсот лет. Существует якобы египетский вариант числа "Пи" ≈ 3.16. Но как мы уже сказали, в "попугаях" вычислить число "Пи" невозможно.

Для того, чтобы понять какое число нам предлагают.

Сделаем простейшее вычисление 4√100 ≈ 3.162277660168379. Или √10 ≈ 3.1622776601683795.  В данном случае можно предположить попытку формально определить число "Пи" без дополнительных расчётов, квадратуры круга (без круга). Мы вычисляя свой алгоритм решая задачу квадратуры круга получили свой результат постоянной = 3.12.

Таким образом основную философскую школу мы имеем греческую.

Вообще числа 1, 2, 3, 4 у пифагорейцев составляли весь числовой ряд и образовывали тетраксис, или четверку. Сумма же чисел, образующих тетраксис, равен десяти (1+2+3+4=10).

Математическая сторона пифагорейского учения о числе:

1, 2, 3, 4, 5,…………………..(разность d = 1),

1, 3, 5, 7, 9, ………………….(разность d = 2),

1, 4, 7, 10, 13,………………..(разность d = 3).

Треугольные числа 1, 3, 6, 10, 15;

Квадратные числа 1, 4, 9, 16, 25;

Пятиугольные числа 1, 5, 12, 22, 25 и т.д.

Вопросы, связанные со свойствами простых чисел исследовал юрист-математик Пьер Ферма (1601 – 1665). Он высказал предположение, что простыми являются все числа вида 2 в квадрате в степени n + 1. Теорема Ферма оказалась верной только для пяти последовательных простых чисел 3, 5, 17, 257, 65537, а шестое число 4294967297, как удалось выяснить математику Леонарду Эйлеру, оказалось составным, потому что делится на 641.

До сего времени никому не удалось установить, имеются ли простые числа вида 2 в квадрате в степени n + 1 при n большем 4. Но эти попытки считается делать не целесообразным, как и народная забава вычислить как можно больше цифр после запятой в числе "Пи" ни к чему ни ведут.

Древние уверяли, что Пифагор знал законы колебания струны монохорда и построения музыкальных созвучий. Один из этих законов гласит, что: Две звучащие струны дают консонанс лишь тогда, когда их длины относятся как целые числа, составляющие треугольное число 10=1+2+3+4, т.е. как 1:2, 2:3, 3:4.

Имея современные знания можно определять сколько угодно вариаций по вычислению таблицы Пифагора, когда средней точкой числового ряда таблицы является цифра 5, где равно удаленные от центра цифры в сумме составляют число 10: 4+6=10; 3+7=10; 2+8=10; 1+9=10.

Таким образом, число 10 , присутствующее в каждой цифровой комбинации определяет одну законченную фазу, одно целое или одну форму развития, которую графически можно обозначить в виде квадрата или круга, имеющего градацию в 360˚. Когда, как уже было сказано 4√100 ≈ 3.162277660168379.

Сама же таблица Пифагора имеет не только линейные и квадратные, но и угловые измерения, которые используются в геометрии, астрологии, системном построении мироздания. В проявлениях целостности, дуализма, тройственности и далее, когда выстраивается порядок системных отношений в системах Бытия дуализма, трехмерного пространства и далее по уровням 4-х, 5-ти, 6-ти и далее мерного мира тонких материй.