Прогрессивная математика

НАЧАЛО

ЧАСТЬ 2

НЕРАЗГАДАННЫЕ ТАЙНЫ

О чем мечтал Ариабата?

Какой звезды он видел свет?

И в строках древнего трактата.

Оставил нам он свой ответ.

К настоящему времени, на примере рассуждений математика Алексея Савватеева мы можем видеть, что наука ушла далеко от тех вычислений которые две тысячи лет назад делал древний астроном Ариабата и до миллиона цифр после запятой числа Пи считает современный компьютер.

Все давно известно и посчитано, но вот понадобилось мне уточнить какие параметры исследовал древний ученый при вычислении числа Пи. Результат поисков меня удивил, когда читая материалы диссертаций ученых физ-мат наук, то там имеются утверждения, что Ариабата своих вычислений не объясняет.

И есть ссылки на работы более позднего древнего астронома Аль-Хорезми, который ссылается на трактат Ариабаты, но делает странные на мой взгляд выводы. Он не смотря на то, что Ариабата по мнению многих вычисляет Пи = 3,1416, применяет в своих вычислениях более привычное древним философам √10 ≈ 3.16.

Почему? Чтобы разобраться в этом, надо смотреть работы древнего астронома. Примерный смысл сказанного (в переводе) древним астрономом: "«Это приближение, а не доказательно, и никто не настаивает на их истинности и никто, кроме Аллаха, не знает истинную длину окружности ... и только Аллах может знать истину».

Заинтересовавшись о какой истине, которую знает только бог, говорит древний астроном Аль-Хорезми, я более детально посмотрел имеющиеся в интернете материалы и нашел, что могло на мой взгляд смутить великого мыслителя древности, который использует √10 ≈ 3.16, не смотря на уточнение Ариабатой  ранней величины Пи до значения 3,1416.

Что же мы видим у Ариабаты? Он предлагает произвести ряд математических действий: "Прибавьте четыре к сотне, затем умножьте результат на восемь и прибавьте шестьдесят две тысячи. ((4 + 100) х 8 + 62000)/20000 = 62832/20000 = 3,1416).

Что здесь могло не понравиться более позднему астроному ?

О чем может сказать вычисление:

62832/20000 = 3,1416

Левая часть выражения показывает на число 62832, а правая на число 31416, которое в два раза меньше левого числа, и становится понятно почему Ариабата берет круг с радиусом 10000. Все говорит о том, что Ариабата не вычислял, а использовал уже известные ему числа, когда количество нулей в диаметре круга влияет на место запятой числа "Пи".

ПАРАДОКС,  - событие, которого быть не может.

Ариабата нашел парадокс, который объединяет разные уровни системы миро строения. Не мудрено, как так выразился Аль Хорезми, что один бог знает, что вычисляет Ариабата. Потому, что сокращая ноли  в знаменателе мы получаем  62832/2 = 31416

Когда это вычисление ломает привычную картину древнего мира. И получается, что древний астроном рисует схему, к которой современная наука только подходит, судя по имеющимся публикациям. Скорее Ариабата создает справочную конструкцию, для любых расчётов при вычислении орбиты космического объекта.

При этом приближение √10 ≈ 3.16 в этой конструкции = 63244/20000=3,1622,

Наше вычисление квадратуры = 3,1249 будет здесь  = 62498/20000=3,1249,

Вычисления Ариабаты = 3,1416 будет здесь = 62832/20000=3,1416...

Как считал две тысячи лет назад? Непонятно, но создал  конструкцию, когда всегда известна длина окружности, от которой можно производить расчеты.

КАКИЕ ТАЙНЫ ХРАНЯТ МАСОНЫ

На вопрос почему увидев в древних вычислениях расчет корня квадратного из 10=3,16, мы говорим что это фальсификация, потому что этот расчет не имеет внутреннего содержания и как маркер, к задаче квадратуры круга ни какого отношения не имеет. Как и теорема Линдемана не имеет ни какого отношения к "античным задачам".

Говорят, что следы задачи о квадратуре круга встречается впервые в греческих сочинениях V в. до н.э. Когда  Плутарх рассказывает, что астроном Анаксагор (500 – 428 г. до н.э.) находясь в тюрьме, отгонял печаль размышлениями над задачей о квадратуре круга. А ни один современный ученый не получил бы инициации в пифагорейское содружество.

Последним кандидатом в сообщество пифагорейцев был норвежский математик Нильс Абель (1802-1829 г.г.), который по слухам одну из спорных задач решил. Хотя это решение наука не признала.  Имея общий научный вывод, что античные задачи не разрешимы.

Говоря о древних вычислениях надо сказать, что кроме шести векторной Вавилонской системы счета, которую  усовершенствовал Пифагор представивший миру свою таблицу, оформленную в стиле римского капитула, мы не видим больше ни каких расчетов. Ни по календарю индейцев майя, ни по египетским, ни по буддийским таблицам расчетов.

Обратимся к "материнской" пифагорейской системе знаний, в которой весь числовой ряд представляет 1, 2, 3, 4. Сумма же чисел, образующих тетраксис, равен десяти (1+2+3+4=10), когда средней точкой числового ряда таблицы является цифра 5, где равно удаленные от центра цифры в сумме составляют число 10: 4+6=10; 3+7=10; 2+8=10; 1+9=10.

Математическая сторона пифагорейского учения о числе:

1, 2, 3, 4, 5,…………………..(разность d = 1 и т.д.).

Треугольные числа 1, 3, 6, 10, 15;

Квадратные числа 1, 4, 9, 16, 25;

Пятиугольные числа 1, 5, 12, 22, 25 и т.д.

Главные тайны пифагорейцев, которые как оказалось знают только масоны. Это первая геометрическая фигура - трех угольная пирамида из четырех шаров. И тетраксис треугольное число состоящее из 10 точек, но если мы соединим все эти точки линиями ограничивающие треугольник. То мы увидим скрытую ранее невидимую суть тетраксиса.

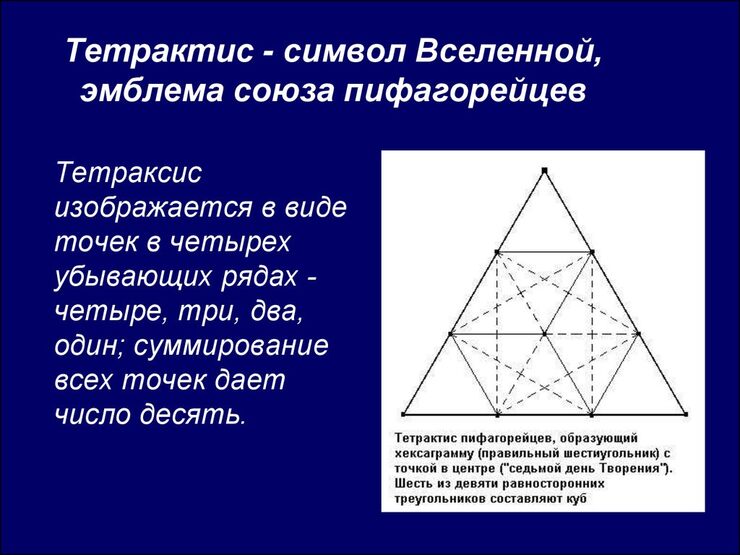
Девять внутренних треугольников вписанных в ограниченную фигуру из десяти точек. А теперь определим аналоги двух фигур, которые требуется построить и видим, что и круг и квадрат имеют центр, вокруг которого они построены. Обе эти геометрические фигуры имеют градацию внешнего периметра равную 360˚.

Поэтому древние делали простейшее вычисление 4√100 ≈ 3.162277660168379.  Казалось бы чем это вычисление отличается от √10 ≈ 3.1622776601683795. Отличие в том, что из 100 можно построить  классический  квадрат, а из 10 квадрат не построить. Все ранее существующие вычисления так же из этой серии, когда 4/3 в четвертой степени 256/81=3,16.

В комедии « Птицы » (414 г. до н.э.) знаменитый греческий поэт Аристофан, шутя на тему о квадратуре круга, вкладывает в уста Астронома Метона следующие слова:

Возьму линейку, проведу прямую,

И мигом круг квадратом обернётся...

Что по нашему разумению должен сделать настоящий ученый? Он не занимаясь плутовством с помощью извращенного разума, должен взять в руки линейку и циркуль и "тупо" выполнить требования условия задачи состоящее из пары десятков слов. Построить квадрат (100), и на гипотенузе отмерить от угла 9 частей.

От центра это будет 4 части, которые и определяют радиус круга, равновеликого квадрату на котором его построили. В ноль, без всякого "Пи".

И надо полагать, что только поэтому имея вычисления 4√100 ≈ 3.16.  Древние астрономы при необходимости писали  √10 ≈ 3.16. А далее в зависимости от параметров расчетов, применяли нужные поправки.

АНТИЧНЫЕ ЗАДАЧИ

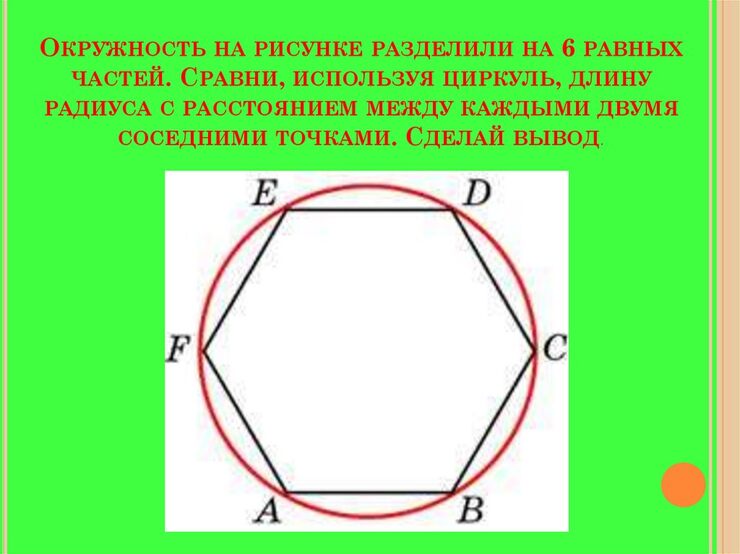
Задачи, которые наука считает неразрешимыми, в принципе своем нами решены. Как решается задача квадратуры круга показано выше. Древние строители с подобными задачами справлялись легко, с помощью мерной веревки или "пояса архитектора". Но в условиях задачи построение нужно делать с помощью линейки и циркуля.

Без лишних расчетов покажу только технику построения трисекции угла. Отмеряем равные отрезки от вершины угла, и делим угол пополам медианой на основание треугольника. Затем основание полученного треугольника превращаем в сторону равностороннего треугольника направленного вершиной вниз. А затем найдя центр построенного треугольника, описываем вокруг него окружность.

В эту окружность вписывает второй зеркальный треугольник вершиной в другую сторону, получилась "Звезда Давида", верхний луч которой делит изначальный угол на три равных части.

Задача удвоения куба сложнее, но тем не менее тоже решаема.

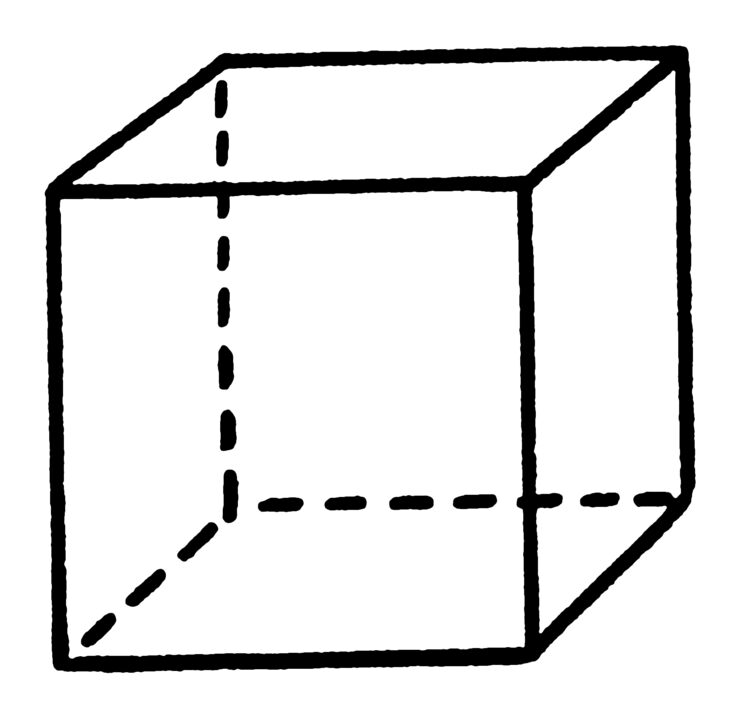
Из античных философов только Архимед имел возможность проверить правильность решения этой задачи. Речь идет об "Архимедовой ванне", в которую опытным путем стесывая грани куба на нужную величину, и погружая в ванну, можно было определить правильность расчетов. Но тесать камень показалось слишком сложно и он решая эту задачу придумал пружину, но задачу не решил.

Чего только не делали древние философы изобретая новые способы вычислений площади геометрических тел, но решить задачу не смогли.  Мы ее решили через двадцать лет, самой последней, практически случайно увидев вот такую конструкцию в которой диагонали делят площадь квадрата на четыре равных части. А дальше дело техники,  увеличить  сторону искомого куба на четверть и задача будет решена...

4 х 4 х 4 = 64   ...   ...   5 х 5 х 5 = 125...   все в допустимой погрешности, когда четырех метровых алтарей не бывает, а в каких единицах нужно было считать мы не знаем. Мы сейчас можем все измерить до одного сантиметра, а приближать это к античному миру не корректно (в локтях (0.4 м) это будет приблизительно о.4 х 0.4 х 0.4 = о.064 ...  0.5 х 0.5 х 0.5 = 0.125).

А если длина локтя не о4 м., а 0,3 или 0,5 метра?

Тут логика простая. Если человек знает как число возводится в куб, то прибавляемая часть к грани куба, проходит ту же процедуру расчетов, что и сам алтарь. Если люди не знакомы с математикой и не могут выполнить расчет увеличения куба, то "ванна Архимеда" остается единственным мерилом .

Картинки взяты в интернете.