
Проблема Гольдбаха - одна из старейших нерешенных математических задач с бородой в 279 лет (на нынешний 2021-й год). И судя по всему, бороде еще расти и расти. Гипотеза Гольдбаха отличается исключительно простой и понятной формулировкой:
любое четное число, начиная с 4, можно представить в виде суммы двух простых чисел.
А собственно проблема состоит в том, что никому не удается ни доказать, ни опровергнуть гипотезу Гольдбаха.
Напомню, что простыми считаются числа: 2, 3, 5, 7, 11, 13 и далее каждое натуральное число, которое не делится без остатка на другие натуральные числа, кроме как на себя и единицу.
Нетрудно видеть, что 4=2+2, 6=3+3, 8=3+5. А 10 имеет даже два представления: 10=3+7=5+5. Увы, доказать возможность разложения для любого четного числа так и не удалось.

Исторически дело обстояло следующим образом. Немецкий профессор математики Кристиан Гольдбах (1690-1764), с 1725 г. трудившийся в России, в 1742 г. в письме к Леонарду Эйлеру предположил, что каждое нечетное число, большее 5, можно представить в виде суммы трех простых чисел.
Швейцарский математик Л.Эйлер (1707-1783), также вовсю вкалывавший в России, заинтересовался проблемой. Еще бы! Позже мало кто из математиков прошел мимо. Эйлер даже выдвинул более сильную гипотезу и не сомневался, что ее можно будет доказать как теорему: каждое четное число, большее двух, можно представить в виде суммы двух простых чисел, т.е. то, что ныне и называется проблемой Гольдбаха.

Поэтому правильнее было бы называть проблему Гольдбаха проблемой Эйлера по имени подлинного автора, что тоже нередко делается в литературе. Но именно Гольдбах поднял весь шум, и без него, наверное, не было бы догадки Эйлера.
Ни великий Эйлер, ни все великие и не очень великие математики так и не решили проблему Гольдбаха. В 1900 г. она под номером 8 вошла в знаменитый список проблем Гильберта, нерешенных к тому времени, но и это не помогло ее решению.

Лишь в 1930-е годы советский математик Л.Шнирельман осуществил громкий для того времени прорыв, доказав, что всякое натуральное число, превышающее единицу, представимо в виде суммы не более 800 тысяч простых чисел. Позже разными исследователями результат улучшался и в 1995 г. был доведен до шести слагаемых.
В 2013 г. наконец-то пал вариант, сформулированный собственно Гольдбахом о представлении нечетных чисел в виде суммы трех простых. Добил его перуанский математик Х.Хельфготт (р.1977). Но классическая гипотеза о разложении четных чисел на пару простых устояла.

Развитие ЭВМ позволило делать такие расчеты, о каких математики прошлого не могли и мечтать. Фактический численный материал помог не только быстро отбросить одни гипотезы, но и выдвигать новые.

На 2012 г. гипотеза Гольдбаха (а точнее, Эйлера) посредством распределенного поиска, т.е. с использованием огромного количества компьютеров, была проверена для всех четных чисел до
4 000 000 000 000 000 000
(4 на 10 в 18-й степени).
Увы, если опровергающего примера не нашлось, то это мало что означает, и лишь побуждает к новым поискам в надежде, что успех рядом. Сомнительная практика! Так же с молитвами: если Господь не откликнулся, значит, плохо молились, и надо молится еще. И так до бесконечности. Поэтому по крайней мере в науке ищут другие подходы.
Я тоже не прошел мимо проблемы, но ограничился только новыми гипотезами. Вообще, заниматься нерешенными математическими задачами - это очень непрактичное занятие и особенно губительное для дилетантов, поскольку оно затягивает подобно наркотику, ведет к неоправданным потерям времени, а то и к помешательству.

Из-за нерешенности проблемы Гольдбаха можно подумать, что разложения четных чисел на пару простых редки как жемчужины в море, и найти их архитрудно. Собственно, так и было в докомпьютерную эру. Однако, к своему удивлению я обнаружил, что каждое число вовсе не ограничивается одним, двумя или тремя разложениями.
Для чисел до 1000 рост количества разложений не так уж трудно было заметить даже тысячу лет назад, и наверняка он не был секретом для Гольдбаха с Эйлером. Но для чисел до 10000 уже нужно около четверти миллиона сложений простых чисел. Столбиком на бумажке это заняло бы год напряженного труда. Для ста тысяч не хватит жизни.

А для 100 миллионов даже компьютеру с миллиардом операций в секунду у меня понадобилось несколько суток. В рамках этих 100 млн в основном делаются нижеследующие выводы, часть из которых, в виде весомых гипотез можно распространить на все числа до бесконечности. Насчиталось вот что.
В 1-й сотне максимальное количество представлений 9 имеет число 90:
90 = 7+83 = 11+79 = 17+73 = 19+71 = 23+67 = 29+61 = 31+59 = 37+53 = 43+47.
В 1-й тысяче максимальное количество представлений 52 имеет число 990.
В первых десяти тысячах максимальное количество представлений 329 имеет число 9240.
В первых ста тысячах количество разложений одного числа доходит до 2168.
В 1-м миллионе до 15594,
в десяти миллионах - до 124180,
в сотне миллионов - до 931793,
а далее быстро переваливает через миллион.
Так что скорее надо говорить о трудности промахнуться в море всевозможных разложений.
Но для проблемы Гольдбаха важны не столько максимальные, сколько минимальные количества разложений. Ведь опровергнуть гипотезу способно всего-то одно противное число, и куча разложений для остальных чисел уже не поправит дело.
Однако, нижние границы количества разложений тоже быстро нарастают! В интервале от 1000002 по 2000000 каждое четное число имеет не менее 3963 разложений, в интервале от 9000002 по 10000000 не менее 26252 разложений.
Числа с малым количеством разложений - это вообще редкость.
Только числа 4, 6, 8 и 12 имеют по единственному представлению в виде суммы 2 простых.
Только 9 чисел имеют по 2 представления:
10, 14, 16, 18, 20, 28, 32, 38, 68.
Например, 10=3+7=5+5, 68=7+61=31+37.
Только 11 чисел имеют по 3 представления:
22, 24, 26, 30, 40, 44, 52, 56, 62, 98, 128.
Также 11 чисел имеют по 4 представления:
34, 36, 42, 46, 50, 58, 80, 88, 92, 122, 152.
Только 16 чисел имеют по 5 представлений и все они находятся в интервале от 48 по 188.
Также 16 чисел имеют по 6 представлений и находятся в интервале от 60 по 332.
Отсюда сразу можно выдвинуть ряд гипотез. Например, что все четные числа более 332 имеют не менее семи разложений в виде двух простых чисел, а каждое четное число более миллиона имеет не менее 3963 разложений. Для сравнения, Гольдбах с Эйлером гораздо скромнее утверждали о существовании хотя бы одного разложения.
А вот минимальные и максимальные количества представлений на промежутках длиной в миллион:
4 - 1000000: 1 и 15594,
9000001 - 10000000: 26252 и 124180,
99000001 - 100000000: 215876 и 925875,
999000001 - 1000000000: 1699409 и 7531017,
9999000001 - 10000000000: 13640853 и 59206649,
99999000001 - 100000000000: 111793975 и 473687623,
999999000001 - 1000000000000: 932731052 и 4102056076.
Кроме того, количества посчитаны на каждом (всего их 200) миллионном промежутке до 200 млн, на графике выглядит так:
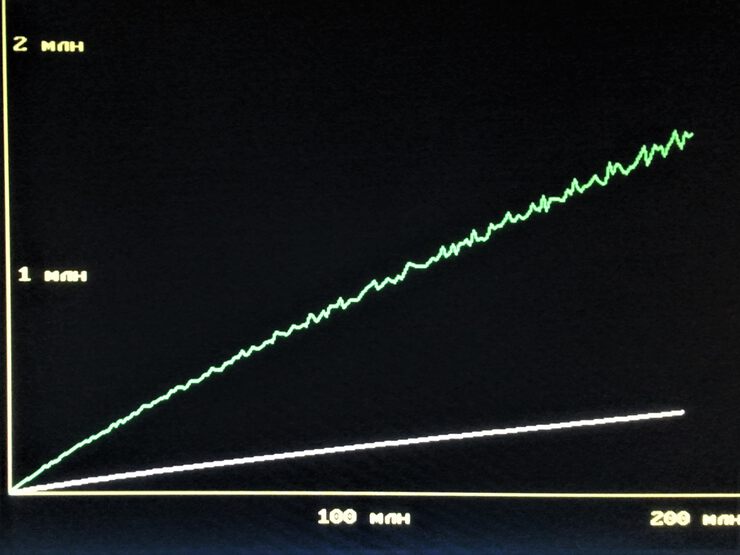
Белая линия - это минимальные значения, зеленая - максимальные.
Максимальные значения несколько скачут, а более важные минимальные неуклонно и плавно растут пропорционально x/ln(x)/ln(x), т.е. аргументу, поделенному на квадрат его логарифма. Конкретнее:
x/ln(x)/ln(x)*0.7259,
где x - середина очередного миллионного интервала.
С 10-го миллиона погрешность указанной функции не превышает 2%, и на графике функция визуально не отличима от белой линии.
Поскольку логарифм, даже в квадрате, меньше любой степенной функции с положительным показателем, то первую скрипку играет сомножитель x, и график мало отличим от линейной функции.
Повторю, что распространение того же закона x/ln(x)/ln(x) на все числа - это, конечно, только гипотеза, но ничуть не менее обоснованная, чем собственно гипотеза Гольдбаха и Эйлера. Ведь поведение простых чисел не зависит от чьих-то желаний, вероисповедования и политической обстановки. У инопланетян и во всей Вселенной будут в точности те же математические законы. Поэтому если уж сами числа решили действовать по какому-либо статистическому закону, то скорее солнце упадет в море, чем числа отрекутся от этого закона.
Древние люди тоже не могли быть уверенными, что солнце взойдет очередной раз, хотя ранее оно делало это регулярно. Только с изучением ядерных реакций и открытием законов развития звезд стало возможно квалифицированное предсказание далекого будущего Солнца и всей Солнечной системы. Так и раскрытие законов простых чисел ставит все дело намного выше простого перебора.
Таким образом, количество разложений на пары простых чисел быстро растет. Это наводит на мысль, что для разложений можно обойтись лишь малой частью простых чисел. Например, число 11 можно безболезненно выкинуть, и оставшихся простых чисел хватит, чтобы гипотеза Гольдбаха продолжала торжествовать на первых 100 миллионах четных чисел, а вероятно и дальше. Но это уже отдельный вопрос, о котором речь пойдет позже. В других статьях наряду с математическими задачами речь пойдет также об ошибках, наделанных математиками и программистами.

Авторская публикация. Свидетельство о публикации в СМИ № J108-49596.
Обсуждения Проблема Гольдбаха
Чтобы быть ученым, надо быть немного сдвинутым. Поэтому неудивительно, что многим из них что-нибудь мерещится, например, ошибочные доказательства, которых в истории не счесть.
А вообще, сомнение - это признак образованного человека. Наоборот, неучи не сомневаются в своих познаниях.
А с утюгами тут немало народа, только они называют их не утюгами, а более ласкающими слух субстанциями.
Поскольку никто не хлопал в ладоши от получения этой мудрости и все столь же упорно отмалчивались, то коллега приходил к выводу, что его не понимают, и вообще все тупые до предела. А потому раздавал свои поучения вновь и вновь, дабы образумить темное человечество.