
П.Ферма (1601-1665) придумал и решил множество математических задач, но знаменит он стал не этим, а, наоборот, той задачей, с которой не справился сам, и над которой безуспешно бились математики и дилетанты в течение 300 лет. Это так называемая Великая теорема Ферма. На сегодня она считается решенной, но сам я не проверял и сильно сомневаюсь в существовании корректного доказательства.
Как показано в предыдущей статье, даже дотошные профессионалы иногда оказываются неспособны переписать без ошибок десяток чисел. Тем более, нереально сделать доказательство в сотню страниц. Еще хорошо, если ошибка выявится в 1-й же строчке, как нередко бывает даже в серьезных статьях. Гораздо хуже, если на изучение уйдут годы. А поскольку проверяльщики тоже могут ошибаться, то их старания мало что гарантируют.
Так что на проблему Ферма не стоит тратить время. Но есть весьма любопытная ставшая достоянием общественности задача от Ферма, которая поддается полной проверке, и на которой специалисты тоже умудрились напортачить.
В 1970 г. в журнале "Техника - молодежи" (N 4) была опубликована следующая заметка.

Увы, напечатанное в журнале решение неверно и именно в таком виде оно отметилось в последующей истории математики. Скорее всего, это вина не Ферма, а работников журнала, потерявших цифру в середине последнего числа.
Итак, задача Ферма состоит в нахождении прямоугольного треугольника с целочисленными сторонами, где гипотенуза есть квадрат целого числа, и сумма катетов есть квадрат некоторого целого числа.
Вообще, прямоугольные треугольники с целочисленными сторонами известны с глубокой древности. Простейший из них: так называемый египетский треугольник со сторонами 3, 4 и 5. Он использовался на практике для получения прямого угла.
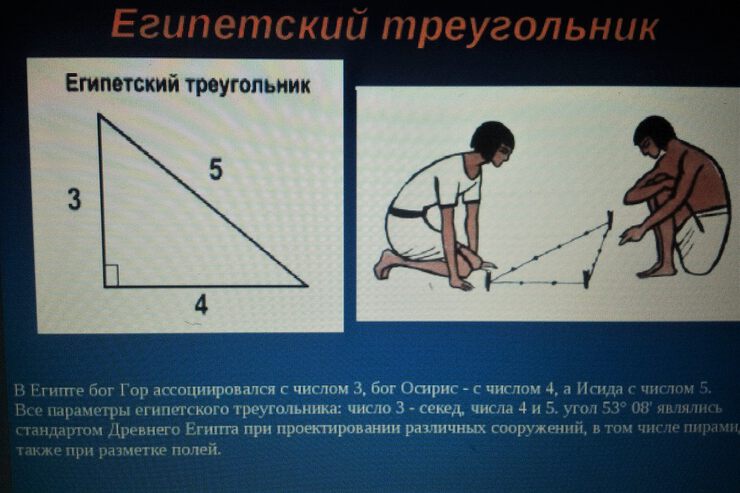
Сегодня, конечно, используются другие инструменты. И задача Ферма не представляет заметной научной или практической ценности. Но она часть нашей истории и по-прежнему интересна в учебном и спортивном плане, как и всякая добротная хитрая задачка.
Известен общий метод для составления прямоугольных треугольников с целочисленными сторонами. Он основан на тождестве:
(a-b)**2 + 4ab = (a+b)**2
Для сторон приняты формулы: X=mm-nn,Y=2mn, Z=mm+nn, где m,n - натуральные числа.
При m=2 и n=1 получим египетский треугольник, при m=3 и n=1 треугольник со сторонами 8, 6, 10, но он мало интересен, поскольку получается удвоением сторон египетского. А вот при m=3 и n=2 получаются стороны 5, 12, 13. При m=4 и n=1 будет: 15, 8, 17.
Разумеется, выписанные здесь треугольники не годятся в качестве решения задачи Ферма, хотя бы потому, что их гипотенузы не являются квадратами целых чисел. Впрочем, пропорционально увеличивая все стороны, совсем нетрудно получать нужные гипотенузы. Например, треугольник: 15, 20, 25.
Гораздо труднее, но реально подобрать, чтобы сумма катетов была квадратом целого числа. Например, треугольник: 9, 40, 41. И еще: 133, 156, 205.
Но чтобы выполнить все требования задачи Ферма, простой перебор не поможет. Неудивительно, что коллеги Ферма не справились с задачей. Впрочем, Ферма дал только ответ, и неизвестно, как он умудрился найти его без ЭВМ.

Вот решение, еще в давние времена вычисленное и проверенное мною на компьютере, а также указанное в Википедии в статье "Пифагорова тройка":
X=1061652293520, Y=4565486027761, Z=4687298610289.
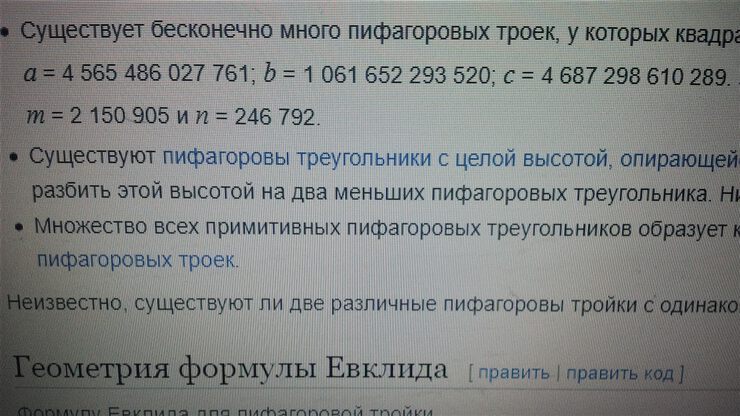
Наверняка, неудачники Френикль и Сен-Мартэн были в шоке. Ведь если искать эти три числа простым перебором, то и поныне никакая ЭВМ не осилит его ни в какие исторические сроки.
Сегодня найдены и другие решения, удивляющие гораздо большим количеством цифр. Известно также, что задача Ферма имеет бесконечно много решений.
Ферма не оставил после себя систематических исследований, он сообщал лишь результаты удивленным современникам. Возможно, поэтому он остался столь загадочной фигурой. Стоит все объяснить, и сразу становится скучно. Для сегодняшних специалистов задача Ферма не представляет трудностей в теоретическом и соответственно в вычислительном плане. Как принято говорить, задача решается элементарными методами. Но элементарные методы не отменяют громоздких вычислений, в которых на каждом шагу предоставляются широкие возможности наделать ошибок.
Наверняка, Ферма не мог увидеть численные решения из тысяч знаков. А мы теперь можем!

Вот очередные по размерам треугольники со взаимно простыми сторонами:
2)
X = 214038981475081188634947041892245670988588201 (45 цифр),
Y = 109945628264924023237017010068507003594693720,
Z = 240625698472667313160415295005368384723483849,
X+Y = a*a , Z = c*c
a= 17999572487701067948161 , c = 15512114571284835412957;
3)
X = 101090445912315611189797633103062269281831072658850463814345155519536067859788318450595485833321 (96 цифр),
Y = 90600415152500364825256074903956700803695382187386257981355501221895481526026353330711612866200,
Z = 135748714471099967645098303815413145183510604468779231285462871341558087008619938117875754653321,
a = 437825148963391521638828389137484882137402791039,
c = 368440923990671763222767414151367493861848396861;
4)
X = 463364435981466638655721606795402574490785034897443124170070240200671104946933926803365302534576258476492322816713177661024808525677009601280034178493297316385999153 (165 цифр),
Y = 704093322799308833776272853814930313676549030172246816105298509194049219955867268919807417417483602815295710263978203420907943571429370020707878980026592034112342096,
Z = 842884338294996678212228837815191418234428179249675666444859533148402499591532256435242317441040296075151069741561268252863830134704359471711958336290700625845640625,
a = 34168080993535113552180464917346868292958739991398355562578195440360113112814117057,
c = 29032470413228645503712143213832535500985227130245791625262982715784415755764157625;
5)
X = 1869389268...5499875521 (254 цифры),
Y = 5444606989...7060603200 (254 цифры),
Z = 5756592873...7850595521 (254 цифры);
6) 404869...648601, 429385...695720, 431289...163449 (361,362,362);
7) 145231...550953, 111626...644696, 112567...375625 (535,536,536);
8) 730881...476201, 189095...207000, 202728...976201 (687,688,688);
9) 233399...850161, 325748...165520, 400733...627889 (все по 859 цифр);
10) 671703...332801, 555262...366720, 871494...749249 (все по 1049 цифр);
...
100) 106526...011921, 843144...097200, 135855...531921 (цифр: 105258, 105257, 105258 соответственно).
Обычно в целочисленных уравнениях либо вовсе нет решений, либо есть решения во вполне приличных числах где-нибудь до 1000. И только в задаче Ферма в простейшем решении фигурируют числа в полтриллиона, а для очередного решения в 45 цифр даже специалисты не найдут названия без заглядывания в справочники.
Для сравнения, уравнение a^4+b^4+c^4=d^4 (сумма 4-х степеней чисел a,b,c равна 4-й степени числа d) имеет простейшее решение в целых числах всего-то до полумиллиона: a=95800, b=217519, c=414560, d=422481, найденное совсем недавно и 200 лет не поддававшееся решению ни на бумажке, ни на компьютерах. Причем согласно гипотезе Л.Эйлера (1769 г.) уравнение не должно было иметь решений. Исторически сложилось так, что первым осилил уравнение Н.Элкис в 1988 г., но он вышел на другое решение: a=2682440, b=15365639, c=18796760, d=20615673. Оба решения я проверил на компьютере подстановкой в уравнение.
Несмотря на элементарность, общая формула решений задачи Ферма громоздка, а доказательство тем более. О нем вкратце рассказано в комментарии.
А здесь уместно предположить, что П.Ферма пошел другим, естественным путем, используя упомянутые выше формулы для целочисленных прямоугольных треугольников:
X=mm-nn, Y=2mn, Z=mm+nn.
Так как от Z требуется быть квадратом целого числа, то получается уравнение mm+nn=cc, и снова можно применить указанные формулы:
m=pp-qq, n=2pq, c=pp+qq.
Числа p,q намного меньше. Это сильно сокращает перебор вариантов, дабы сделать X+Y квадратом целого числа. Простейшая пара (p,q)=(1469,84) выскакивает на машине мгновенно. Она и дает авторское решение задачи Ферма. Правда, следующую пару взаимно простых чисел
(p,q) = (123672266091, 14740596026)
компьютер простым перебором найдет только через тысячи лет.
А для очередной пары
(596892949105755111413019,
110271171656540412245450)
не хватит даже возраста Вселенной.
Вероятно, именно таким путем рационального перебора шел Ферма, но естественный путь завел в тупик. Поэтому, найдя одно решение, он не смог найти остальные. А если бы он имел общую формулу, то наверняка не упустил бы случая поудивлять современников огромными числами.

Авторская публикация. Свидетельство о публикации в СМИ № J108-49609.
Обсуждения Задача Ферма
Подоспели проверяльщики, их решенья опрокинули.
К ним прибавились гадальщики, все решения откинули,
Современные фанатики, кое что к чему прикинули,
И в компьютерном журнальчике, их идеи снова хлынули.
Возмущения математиков, переросли в возбуждения решаемых вариантов, появились вариации и вибрации с волновыми цепями треугольных нагромождений, что о вошло в аналы математических легенд. И вот те на-новая теория больших чисел, открыла «золотой век» в арифметической неометрии с тригонометрическим уклоном. Ко всему подключились логики и тут началось подключили спецязык теоретической информатики в обновлённой теории чисел, вспомнили эвклидовскую геометрию, и стали доказывать, 3х3+4х4= 5х5=25 или 25-9=2х2х2х2, а двойка в четвёртой степени, символизирует четвёртое измерение в геометрии. И как объяснить появление такого контраста? Специалисты по информатике ощутили радостное возбуждение, когда разобрались в прогрессе достигнутом при автоматическом подтверждении доказательств в формалистическом подтверждении на практике при условии строгой интепретации теоремы Ферма. С аксилмой выбора согласно Цермело и Френкеля. Естественно без логической дедукции тут не обойтись и при этом не поскандалить с выдумщиками новых правил в математики простых чисел, перемешивая их с комплексными, что подтвеждала в своё время «Арифметика» Диофанта с её «эллиптической кривой». Галуа представил себе несколько иное уравнение с чёткими правилами совокупления и возвышения до безганичных пределов с конечной бесконечностью после модуляции функционала при условии двумерного обобщения знакомых из тригонометрических аналов синусов и косинусов, тангенсов и котангенсов. А когда Кен Рибет подтвердил предположение Жан-Пьера Сера о том, что свойства модулярной функционала, заданного формой эллиптической кривой Фрея, подразумевающей существование нового доказательства, то возникла новая гипотеза с семилетним поиском решения и доказательств непостижимости анализа того что заключено в ПИФАГОРОВЫХ штанах. Что и послужило стартовой точкой открытого диалога, который является слишком неуловимым и живым, чтобы ограничивать его серьёзными пределами, чуждыми данной теме решениями. НАДЕЮСЬ, ЧТО МЕНЯ ПОНЯЛИ.
Итак, X^2+Y^2 = Z^2, X+Y=a^2, Z=c^2.
Замена Y=a^2-X приводит задачу Ферма к уравнению
-(2X-a^2)^2 + 2c^4 = a^4.
Так что дело сводится к уравнению:
-P^2 + 2Q^4 = R^4, (1)
откуда уже X=(R^2+P)/2, Y=(R^2-P)/2, Z=Q^2, a=R, c=Q.
Уравнение (1) имеет тривиальное решение (1,1,1), а далее от каждого имеющегося решения (x,y,z) следующее (а то и сразу два, поскольку в формуле для B два варианта: +x и -x) получается по формулам:
P = ¦8(yzAB)^2 - (2yzAB - y^2*A^2 + z^2*B^2)^2¦ ,
Q = y^2*A^2 + z^2*B^2 ,
R = ¦z^2*A^2 - 2y^2*B^2¦ ,
где A = (2y^2+z^2)/C ,
B = (yz+-x)/C ,
C - наибольший общий делитель для 2y^2 +z^2 и yz+-x .
Причем так исчерпываются все решения со взаимно простыми P,Q,R.
Начав с (x,y,z)=(1,1,1), получим 2-е решение: (P,Q,R)=(239,13,1).
Далее
3) (2750257, 1525, 1343),
4) (3503833734241, 2165017, 2372159),
5) (2543305831910011724639, 42422452969, 9788425919), ...
200) (114875...606401, 972496...105201, 827656...972799) (цифр:
42087, 21043, 21043 соответственно).
1-е, 2-е и 3-е решения уравнения (1) не приводят к решениям задачи Ферма, так как дают Y меньше или равным нулю. А 4-е в самый раз!
Замечание. Каждое решение еще одного интересного родственного уравнения
X^2 + 2Y^4 = Z^4
выражается через другое его решение или решение уравнения (1) по формулам:
X=12y^4*z^4-4y^8-z^8 ,
Y=2xyz, Z=2y^4+z^4 .
Вот его простейшие решения:
1) (7, 2, 3),
2) (7967, 84, 113),
3) (3262580153, 6214, 57123),
4) (60912456065182847, 151245528, 262621633),
5) (83545316896178428367654599, 11265465210550, 14070212996451).