
Математики, как и все люди, ошибаются. Тысячи лет они попусту бились и выдавали на-гора несметное количество "решений" математических проблем, которые, как позже выяснилось, вообще нельзя решить.
Затем ЭВМ помогли выявить массу просчетов в работах, которые считались непогрешимыми. Можно было надеяться, что компьютеры наконец-то наведут порядок. Но не тут-то было! Машины тоже дают сбои, но главным, как и всюду, является человеческий фактор. Можно неправильно загрузить исходные данные, потом неверно интерпретировать результаты, и еще делаются горы ошибок при написании самих программ.
В свое время меня достали ошибки трансляторов, и пришлось делать свой язык программирования. Но он все равно не избавляет от ошибок в WINDOWS и в других операционных системах, а также от сбоев в самом оборудовании.
Рассмотрим пример, показательный как в плане достижений математиков, так и в плане их просчетов. Это как "блеск и нищета куртизанок".

Простые числа важны в теоретическом плане, а в конце XX выяснилась еще их огромная практическая важность для кодирования информации. Кроме того, за достижения в поиске простых чисел не раз объявлялись и присуждались большие премии, не говоря уже о почете и месте в истории.
Исторически сложился интерес к количеству простых чисел в 1-й сотне, потом в 1-й тысяче и т.д. по степеням десятки. До 10 имеется 4 простых числа: 2, 3, 5, 7. В сотне еще добавляются 11, 13, 17, 19 и т.д., и всего их становится 25. Вот табличка интервалов и проверенных мною (с помощью компьютера, конечно) количеств простых чисел в интервалах:
До 10: 4
До 100: 25
До 1 000: 168
До 10 000: 1229
До 100 000: 9592
До 1 000 000: 78498
До 10 000 000: 664579
До 100 000 000: 5761455
До 1 000 000 000: 50847534
До 10 000 000 000: 455052511
До 100 000 000 000: 4118054813
До 1 000 000 000 000: 37607912018
До 10 000 000 000 000: 346065536839
До 100 000 000 000 000: 3204941750802
Так это показывает программа, ведущая расчет:
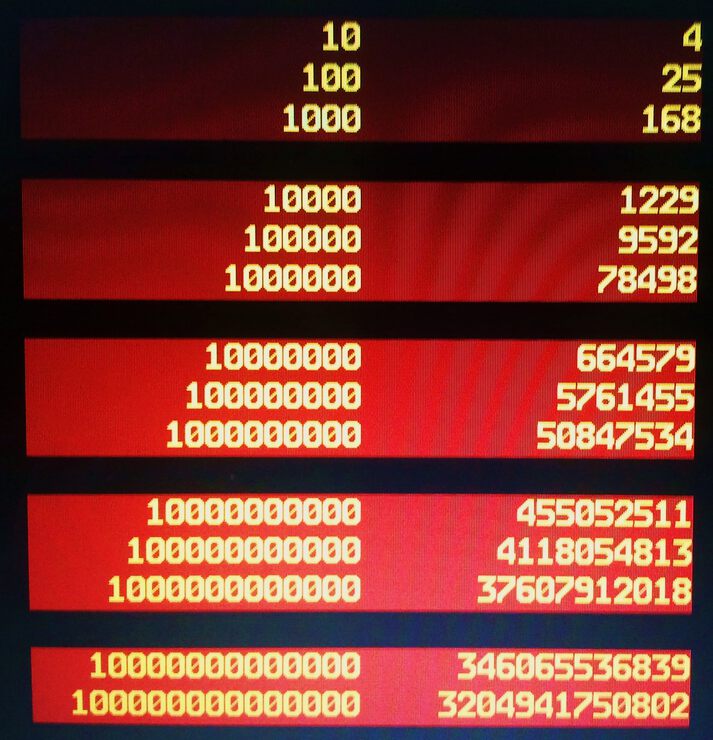
Вопрос о достоверности данных и об ответственности авторов тут далеко не праздный, поскольку с указанной таблицей связано немало ошибок. А ведь это фактический материал, который сам служит для проверки формул и теорий.
Меня заинтересовали этой табличкой в 2002 г. в Уральском университете, где я тогда работал. В то время табличка была короче и содержала не 14 строк, как здесь, а 10, причем в 10-й строке стояло число на единичку больше: 455053512. Тогда еще в бумажной литературе после таблички добавляли: "Вы не представляете себе, какое количество труда потребовалось для составления этой скромной с виду талицы". Вот фото по капитальной книге "Лекции по теории чисел" (Сизый С.В., 1999 г.):

Но, как я только что обнаружил в Интернете, тем же 1999 г. датируется книга Шварца (W.Schwarz), в которой таблица имеет аж 22 строки. Понятно, что в 1999 г. у нас могли не знать об этом достижении, но о нем почему-то не знали и гораздо позже. Больше этого Шварца я не видел, к ошибкам на бумаге в наше время щедро добавились чудеса и глупости Интернета.
Во всяком случае, для меня отправной точкой послужили "Лекции" С.В.Сизого, которые по мнению местных специалистов были последним словом в теории чисел.
Упомянутое в "Лекциях", не указанное точно, количество труда так и осталось загадкой, но я воспроизвел всю тогдашнюю таблицу за 15 минут машинного времени на заурядном персональном компьютере. Сегодня это делается вообще за полминуты. Примечательно, что объем моей программы не превышал 1 Кб (точнее, был 999, а сейчас и того меньше: 871).
Однако, к моему удивлению и удивлению коллег не сошлось последнее число. Проведя расчет еще несколькими способами, я все-таки настоял на своем, и позже в литературе попадалось мое число 455052511. Но в нынешнем электронном варианте книги С.В.Сизого ошибка не исправлена и, наверное, останется на века, чтобы морочить людям голову.
Тогда же я впервые (по крайней мере, в местных кругах) посчитал 11-ю и 12-ю строчки таблицы, на что ушли соответственно часы и дни, поскольку на каждую следующую строку пошло более чем десятикратное увеличения расчетов.
Почти 20 лет я не возвращался к этим вопросам, хотя мне сообщали, что нашлись умельцы, добавившие еще пару строк. О Шварце опять не упоминали. Теперь я наконец-то глянул на эту новую пару строк и в них опять обнаружил ошибку. Вот что написано в Интернете в статье "Сколько всего простых чисел?":
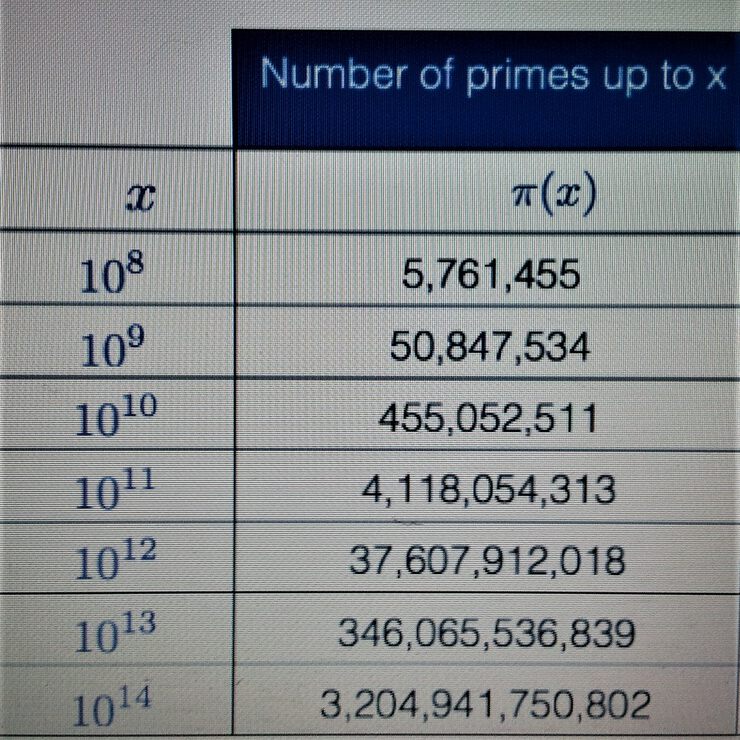
В 11-й строке оказались три последние цифры 313, а правильно 813, что я установил почти 20 лет назад, и на днях еще раз проверил другим вариантом программы и сверил с многими другими литературными источниками.
Но, как говорится, что написано пером, то не вырубишь топором. В Интернете все еще гуляет вариант 20-летней давности с той же ошибкой в 10-й строке. Вот что написано в статье "Первые 50 миллионов простых чисел" (автор Д.Цагир):

Здесь чуть приоткрывается завеса над затратами. Речь идет о "тысячах часов трудоемких вычислений". А на самом деле достаточно одной минуты. Неспециалист эти "тысячи часов" да еще с ошибочным числом вполне может принять за высшее достижение математиков. Правда, впервые статья опубликована в 1985 г. в сборнике "Живые числа: пять экскурсий". Наверное, тогда было вычислять труднее. Но еще с 1960-х годов существовали БЭСМ-6 с миллионом операций в секунду, которым тысячи часов не понадобились бы.
Кстати, за примерами нерациональных расчетов далеко ходить не надо. Очень задумчив WINDOWS, особенно при загрузке. И надо ждать несколько секунд, пока выскочит какое-нибудь мелкостное меню. Для сравнения, мои производственные системы загружаются мгновенно и даже 20 лет назад на гораздо более скромной технике за одну секунду перелопачивали всё, что за годы наработано предприятием, и формировали огромные отчеты в сотни страниц. Есть наглядные общедоступные примеры: интернетовские поисковики - весьма шустрые. Значит, можно делать качественно! Наверное, конкуренция подбодрила. А WINDOWS - это монополист.
Вот еще один перл в статье "Список простых чисел от 1 до 100 тысяч":

В первой же строке статьи указано неверное количество простых чисел 9593, тогда как правильное на 1 меньше. Причем в самом списке фигурируют 9592 числа. Как говорится, не верь глазам своим. Вот и должны гадать читатели, то ли автор ошибся в количестве чисел, то ли пропустил одно число в своем списке. Значит, надо сравнивать с другим источником. А если мнения разделились, то кто прав? Если сам не можешь проверить на компьютере, то получается вопрос веры, а не науки.
В результате такой веры немало исследований, не только в математике, исходило из неверных данных и, естественно, такие же выдавало. Поэтому имеет смысл перерешивать вроде бы решенные математические задачи и устранять ошибки, если таковые найдутся.
На сегодня наиболее полная обнаруженная мной табличка имеет 27 строк и опубликована в Википедии в статье "Функция распределения простых чисел":
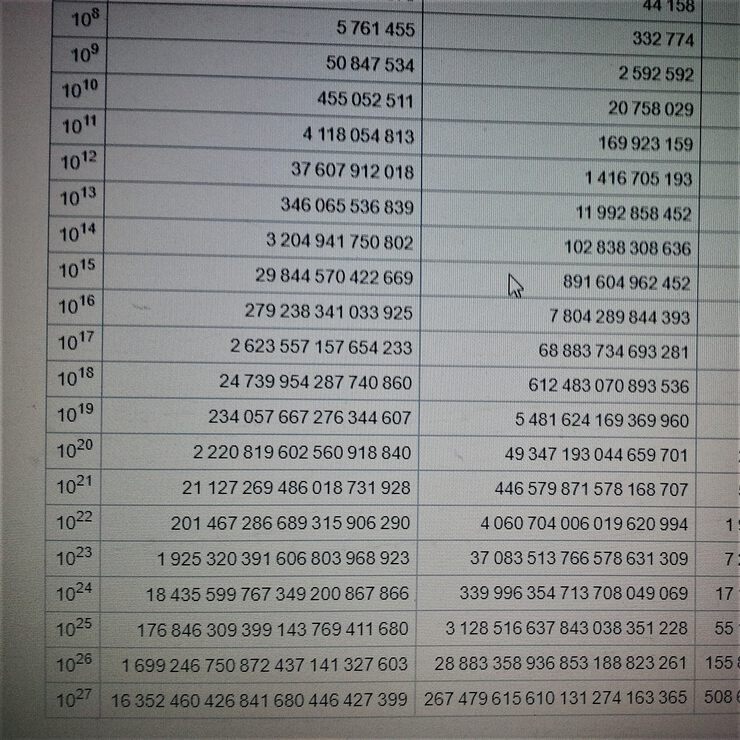
В статье ссылаются на 4 источника, но ни в одном из них всей данной таблицы нет, максимум 25 строк в работе от 2008 г. причем в более поздних работах и того меньше.
Наука - занятие довольно свободное. Например, великий П.Ферма занимался математикой исключительно в свободное от работы время (а работал он юристом). Поэтому обычное дело, когда ученые независимо работают над одними и теми же проблемами и нередко повторяют уже открытое. Хотя что значит открытое? Заблуждений и ошибок в науке горы. Поэтому подтверждение разными источниками делает результаты более надежными и весомыми. Кроме того, исследователи обычно идут своими путями, разрабатывая оригинальные методы, которые нередко годятся потом для других задач.
Здесь приведен только один, но поучительный пример, когда на микроскопических сведениях из десятка чисел наделали ошибок отнюдь не глупые люди. А статьи, которые мне давали на рецензию, нередко кишели глупостями, иногда список ошибок в них превышал объем самой статьи.
Поэтому когда сообщают о доказательстве объемом в 200 страниц для какой-нибудь теоремы, то это лучше понимать так, что какой-то помешанный впустую потратил годы жизни. Конечно, написать можно и 1000 страниц. Но кто это проверит? Нужен еще более чокнутый, который тоже потратит годы, но в отличие от автора не может претендовать ни на какие лавры. Кроме того, не счесть случаев, когда рецензенты не замечали ошибок.

Не поможет также проверка по частям многостраничного доказательства, например, тысячью человек, да и тех не найти. Все доказательство должно уместиться в одной голове. Но где такие головы?

Так что если для теоремы нет короткого доказательства, то можно с уверенностью считать, что его нет вообще.
Разумеется, я тоже ошибаюсь. Но зная, что человеку свойственно ошибаться, потом перечитываю и подправляю написанное 10-20, иногда более ста раз, а расчеты проверяю разными методами и сравниваю с результатами других авторов. Это позволяет качественно снизить уровень брака и принципиально отличается от того, когда энтузиасты понятия не имеют о возможности ошибаться и первое пришедшее в голову считают от Бога, истинным и неподлежащим проверке.
В следующей статье я расскажу еще об одной застарелой плюхе, которую не вырубишь топором.
Авторская публикация. Свидетельство о публикации в СМИ № J108-49603.
Обсуждения Количество простых чисел и ошибки математиков