
Сомнительные рецепты и заклинания давно заполнили массовое сознание, широким фронтом проникли в психологию, общественные и экономические науки. Теперь я с удивлением обнаружил, что они добрались до математики.

Еще со школы мне помнилось, что с помощью циркуля и линейки окружность прекрасно делится на 3, 4, 5, 6 равных частей, А вот на 7, 9, 11, 13 не делится. Так вот, сунулся я в Интернет с запросом "деление окружности на равные части" и, как говорится, узнал много нового!
На множестве сайтов без тени сомнения, хорошо поставленным преподавательским языком, циркулем и линейкой делят окружность на 7 и на любое заданное количество равных частей. Нет, это не муки творчества какого-нибудь двоечника или невежественного дилетанта. А всё идет вперемежку со вполне законными добротными построениями.

Писали профессионалы, не сомневающиеся, что их методы известны еще со времен царя Гороха, и что должно быть стыдно каждому, кто их не знает или посмеет в них усомниться. Кое-где аж под вывеской "Геометрия для чайников"!

Так, в качестве стороны правильного 7-угольника или, что то же самое, хорды при делении на 7 частей окружности радиуса R, там предлагается высота равностороннего треугольника со стороной R. Для единичного радиуса это корень квадратный из 3 и пополам, в десятичной записи 0.8660254038.
Между тем, правильная длина хорды равна удвоенному синусу угла в 360/14 градусов, в десятичной записи 0.8677674782. Вроде бы разница не велика, всего-то две десятых процента. Однако, когда мы отложим 7 хорд, то отличие начальной и конечной точек составит уже 1.4 процента от длины хорды. Для круга радиуса 10 см разница выльется более чем в миллиметр (точнее 1.2 мм).
Для домашнего рукоделия или в школьной тетрадке разница незначительна и может оказаться незаметной. Но в технических устройствах ошибка в 1 мм бывает катастрофична. Например, через миллиметровую трещину из емкости моментально выльется всё ее содержимое. И уж тем более, надо гнать в три шеи бухгалтера, если у него баланс всегда не сходится на 1.4 процента. А может быть, и под суд за хищения в особо крупных размерах!

Кто при проектировании 100-метрового моста ошибется на 1%, того тоже под суд, потому что автомобилям будет неудобственно прыгать через метровую расщелину, если, конечно, мост не рухнет раньше.

Вообще, теория приближенных вычислений - это один из важнейших разделов математики. Погрешность вычислений является там предметом пристального внимания и сама заранее старательно вычисляется. Но никогда приближенное вычисление не выдавалось за точное. Так было. Но теперь уже нет.
Почитал отклики на форумах. Так, ни один человек понятия не имеет о том, что бывают точные построения и приближенные. У них все приближенные. Логика примерно такова: раз число пи мы знаем приближенно, то и все остальное приблизительно.
А ведь вылезли на мировое обозрение не случайные люди, которые как огня боятся математики, а те, кто имеют к ней интерес и считают, что смыслят в ней. Разумеется, никто не заметил ошибок в делении окружности. Так что "наука", пропагандируемая в Интернете, а, наверняка, уже и в школе, дала свои богатые всходы.
Это уже целая культура, в которой не утруждают себя доказательствами, а считают правильным то, что приглянулось, или то, что первым взбрело в голову. Правда, мосты рушились и в прежние эпохи. Но теперь можно ожидать оживление этого процесса.
Ничем не лучше другой интернетовский, якобы универсальный, метод деления окружности на любое количество частей. В нем диаметр на оси ординат делится на n равных частей, а затем через точки деления проводятся лучи из точки (минус корень квадратный из 3, ноль).
Только при n=3 результат точен. При n=7 для второго конца хорды, начинающейся в точке (0,1), вместо правильных цифр (0.7818,0.6235) (это косинус и синус угла 90-360/7 градусов) интернетовский метод выдает (0.7828,0.6223).
Немного из истории вопроса, которая тоже есть в Интернете, но затерялась в необъятном хламе и поэтому осталась незамеченной ни горе-преподавателями, ни учениками.

На 3, 5, 15 частей делил окружность еще Евклид. К.Ф.Гаусс и П.-Л.Ванцель в XIX веке точно выяснили, на сколько равных частей делится окружность циркулем и линейкой, а на сколько не делится. В частности, делится на 17, 257, 65537 равных частей и не делится на 7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25, 26, 27, 28, 29, 31, 33, 35, 36, 37, 38, 39.
Если координаты выражаются через квадратные радикалы, то делится. Для случая 7 нужны кубические радикалы, а они не строятся циркулем и линейкой.
Гаусс особо гордился тем, что нашел метод построения правильного 17-угольника, и даже заказал его изображение на своем надгробии. Но камнетесы отказались это сделать, так как сочли, что рисунок будет невыразительным. (По некоторым данным 17-конечная звездочка все-таки нарисована на постаменте, но на неприметном месте.) А ведь можно было сделать выразительно, например, так:
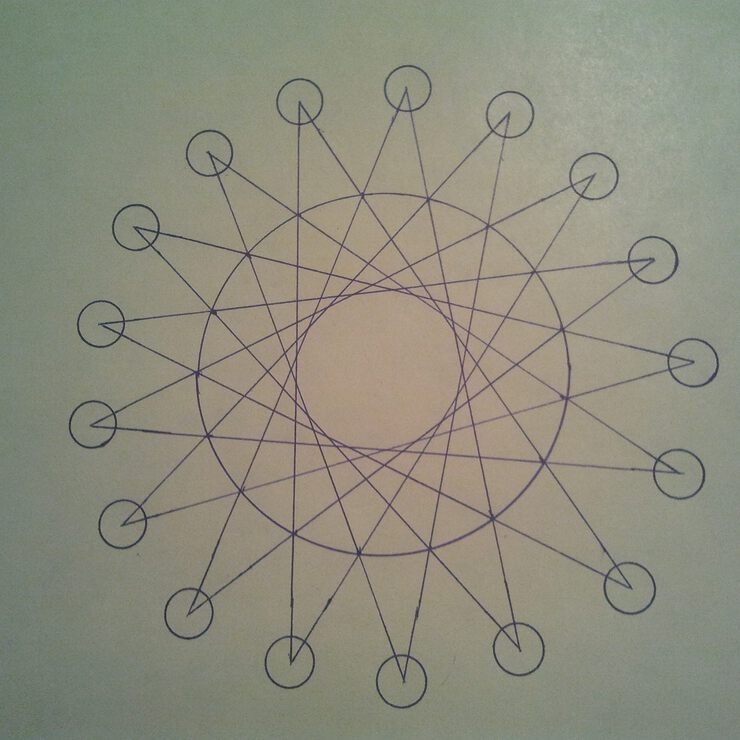
Авторская публикация. Свидетельство о публикации в СМИ № J108-48526.
Обсуждения Бодрое шествие заклинаний