
Г.Дьюдени (1857-1930) - талантливый самоучка, классик занимательной математики, автор множества головоломок, изданных в книгах "Кентерберийские головоломки" (1907), "Математические развлечения" (1917), "Пятьсот двадцать головоломок", "200 знаменитых головоломок мира".
Вот где можно культурно развлечься и объективно проверить качество своего мышления, а не только бить себя в грудь, заявляя о единственно правильном своем мышлении, не осилившем даже школьную программу. Понятно, что высокодуховные светила считают себя выше всякой материи и не опустятся до решения задачек, однако, не отказываются от еды, от компьютера, от комфортного жилья и не торопятся в пещеру.

Приведу только одну приглянувшуюся мне задачку от Дьюдени. В сборнике "Кентерберийские головоломки" под номером 21 идет "Головоломка пахаря". В ней пахарь рассказывает:
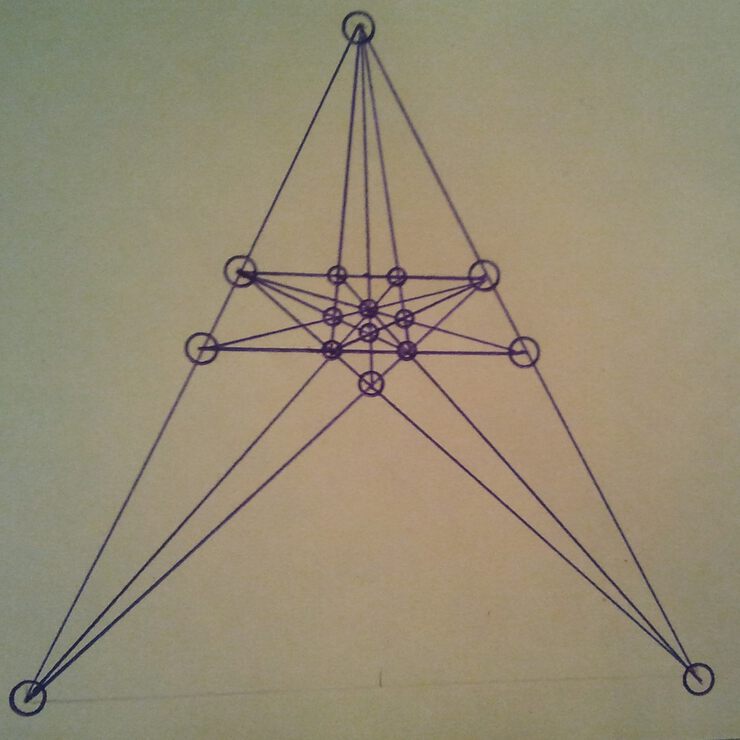
"У одного помещика из Суссекса, откуда я приехал, посажено 16 прекрасных дубов так, что они образуют 12 рядов по 4 дерева в каждом. Однажды мимо проезжал человек большой учености, который сказал, что 16 деревьев можно посадить 15-ю рядами по 4 дерева в каждом. Не могли бы вы показать, как это сделать? Многие сомневались, вообще возможно ли это.
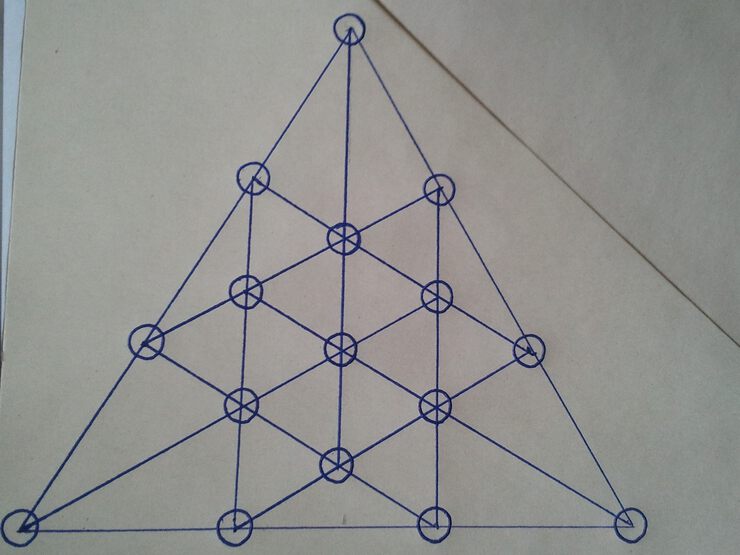
На рисунке показан один из многих двенадцатирядовых способов. А как сделать 15 рядов?"
Ответ Дьюдени таков.
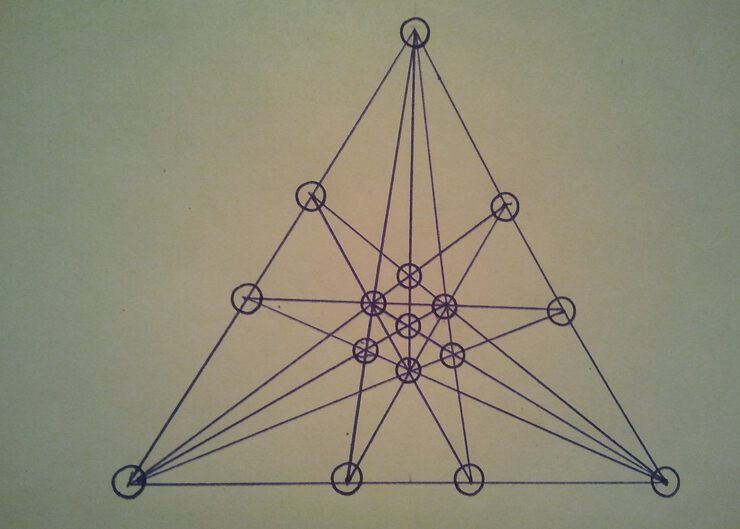
"На рисунке показано, как можно посадить 16 деревьев, чтобы они образовали 15 рядов по 4 дерева в каждом ряду. Это число больше того, которое давно считалось максимальным. Хотя при нынешнем уровне наших знаний невозможно строго доказать, что число 15 нельзя превзойти, тем не менее я свято верю в то, что это максимально возможное число рядов."
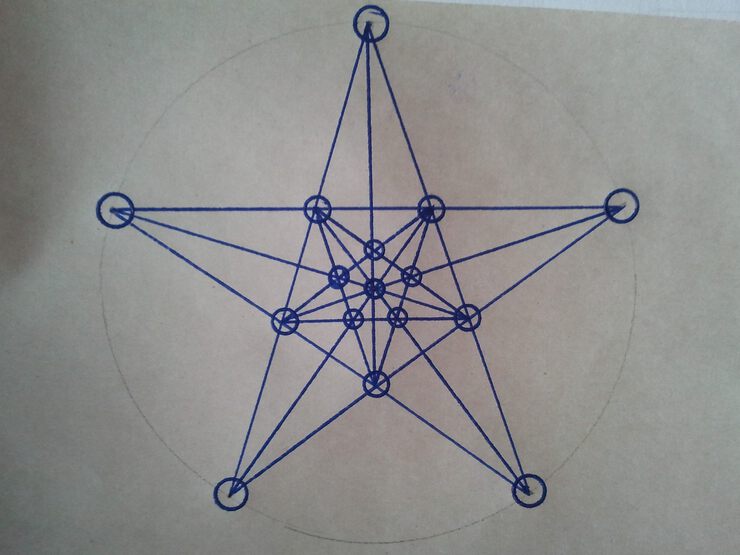
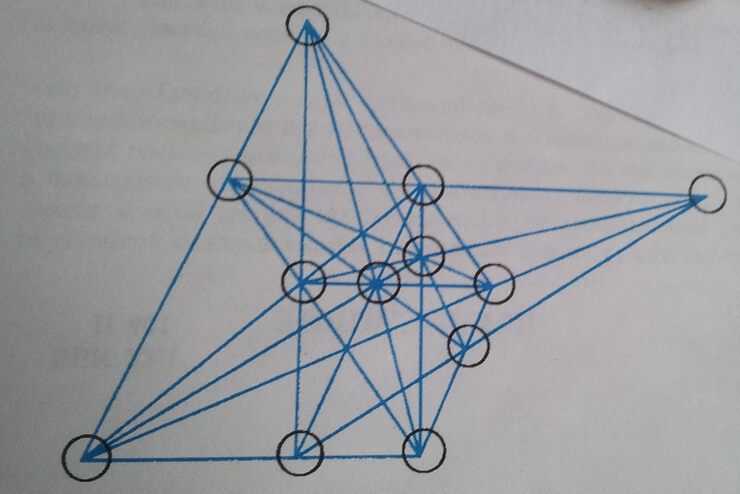
Но размещение Дьюдени не единственное. Мне повезло найти второе решение:
Для контроля координаты:
(0,2), (-2,0), (2,0), (4-2a,0), (2a-4,0),
(2-a,1), (a-2,1), (4a-9,1), (9-4a,1), (0,2/a), (0,2/3), (0,2/(4-a)),
(11-5a,a-1), (5a-11,a-1), ((7a-17)/11,(a+7)/11), ((17-7a)/11,(a+7)/11),
где a = корень квадратный из 5.
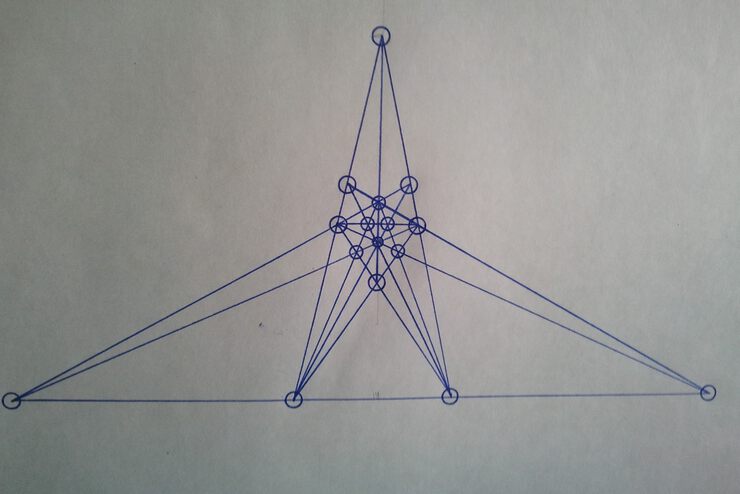
Третье решение:
Координаты точек на нижней стороне равностороннего треугольника:
(-1,0), (2-a,0), (a-2,0), (1,0), где a = корень квадратный из 5.
Остальные точки - на основе соображений симметрии.
Четвертое решение:
(0,2), (-1,0), (1,0), (-1/2,1), (1-a/2,1), (a/2-1,1), (1/2,1),
((a-3)/2,a-1), ((11-5a)/2,a-1), ((5a-11)/2,a-1), ((3-a)/2,a-1),
(0,2/a), (0,10-4a), (0,(8+2a)/11), (2/a-1,2-2/a), (1-2/a,2-2/a),
где a = корень квадратный из 5.
Возможно, и это не конец.
В связи со святой верой Дьюдени можно напомнить родственную задачу о размещении дубов не по 4 в ряд, а по 3. Правда, в оригинале фигурируют не дубы, а шашки. Вообще, точнее во всех этих случаях было бы говорить о точках.
Так вот, при размещении шашек по 3 в ряд автор Г.Винокуров поначалу просил из 11 шашек составить 13 рядов. Однако, очень скоро читатели довели это число до 16 рядов. Позже выяснилось, что по существу представляет интерес задача размещения двенадцати шашек, откуда уже легко вытекают решения для 11.
Размещение 12 шашек в 19 рядов по 3 шашки в каждом:
Если покопаться в старых головоломках, то наверняка можно открыть еще много такого, о чем не догадывались авторы.

Авторская публикация. Свидетельство о публикации в СМИ № J108-48497.
Обсуждения Дьюдени и дубы
Точки на нижней линии:
(-1,0), (-a,0), (0,0), (a,0), (1,0),
где a = 1 / (1 + tg 36 град / cos 18 град) =
= 0.5669152706817990.
По 5 дубов в каждом ряду с меньшей
производительностью возможны размещения:
19 дубов в 9 рядов (треугольником),
25 дубов в 12 рядов (квадратом),
31 дуб в 15 рядов (пятиугольником).
Компьютерный расчет был продолжен до миллиона для K, кратных 30, для лучей из точки (R,0).
Как и в том комментарии, должно быть R=0.5/cos(72 град),
численно R=1.618033988749895
(а не 2cos(пи/10)).
Более 7 лучей нигде не обнаружено.
Кандидат на 13-е решение.
Логическая связь решений.
Формулы ко 2-му решению.
aaa+9aa-a-1=0, a = 0.384042943260.
h1 = (1+3a)/(2+7a+aa), h2=1/2.
Сверху вниз, справа от оси симметрии и на самой оси:
(0,1),
((1+6a+9aa)*aa/(225aa-2a-19), (8a+28aa)/(225aa-2a-19)),
(0, (1+3a)/(2+5a+aa)),
((29aa-2a-3)/(4+10a-14aa), (1+4a+3aa)/(4+10a-14aa)),
((aa-aaa)/(2+6a), 1/2), (a/2, 1/2),
((aa+3aaa)/(3+9a-6aa), (3+10a-3aa)/(15a+51aa)),
(0, (2+7a+aa)/(4+15a+3aa)),
(2aa/(2+7a+aa), h1),
(a-ah1,h1) = ((1+2a-5aa)/(2+7a+aa), h1),
(0, 1/(2+a)), (a,0), (1,0).
Еще любопытна точка ((2+7a+aa)/(1+a), 0), независящая от вариаций h1 и h2. Через нее проходят продолжения двух наклонных рядов, находящихся вверху рисунка.
a - корень кубического уравнения: aaa-aa-9a+1=0.
a=0.1099162641747425.
Сверху вниз. Нижние две точки не вошли в экран.
(0,3), (-2/3,1), ((2a-2)/(9+3a), 1),
((2-2a)/(9+3a), 1), (2/3,1),
(0, (9+3a)/(11+a)),
(-(2-8a-2aa)/(1+34a+13aa), (9a+3aa)/(1+5a+2aa)),
(-(a+2aa+aaa)/(1+5a+2aa), ((9a+3aa)/(1+5a+2aa)),
((a+2aa+aaa)/(1+5a+2aa), ((9a+3aa)/(1+5a+2aa)),
((2-8a-2aa)/(1+34a+13aa), (9a+3aa)/(1+5a+2aa)),
(0, 3/5),
(-(2a+2aa)/(2+5a+aa), (9a+3aa)/(2+5a+aa)),
((2a+2aa)/(2+5a+aa), (9a+3aa)/(2+5a+aa)),
(0, (9a+3aa)/(2+7a+3aa)),
((4a-4)/(13+6a+aa), (3+6a+3aa)/(13+6a+aa)),
((4-4a)/(13+6a+aa), (3+6a+3aa)/(13+6a+aa)),
(-1,0), (-a,0), (a,0), (1,0),
((2a-2)/(1-3a), (-3-3a)/(1-3a)),
((2-2a)/(1-3a), (-3-3a)/(1-3a)).
a - корень кубического уравнения aaa-aa-9a+1=0.
a=0.1099162641747425.
Сверху вниз. Первые две точки не вошли в экран.
((a-1)/2/a, (1+a)/a), ((1-a)/2/a, ((1+a)/a), (0,2),
(-1/2,1), ((a-1)/(6+2a)), 1), ((1-a)/(6+2a), 1), (1/2,1),
(0, (6+2a)/(7+a)),
(-(2-2a)/(9+6a+aa), (6+8a+2aa)/(9+6a+aa)),
(-(6a+2aa)/(9+6a+aa), (6+8a+2aa)/(9+6a+aa)),
((6a+2aa)/(9+6a+aa), (6+8a+2aa)/(9+6a+aa)),
((2-2a)/(9+6a+aa), (6+8a+2aa)/(9+6a+aa)),
(0,2/3),
(-(a+aa)/(1+4a+aa), (6a+2aa)/(1+4a+aa)),
((a+aa)/(1+4a+aa), (6a+2aa)/(1+4a+aa)),
(0, (6a+2aa)/(1+5a+2aa)),
(-(1-2a+aa)/(4-6a-2aa), ((1-4a-aa)/(2-3a-aa)),
((1-2a+aa)/(4-6a-2aa), ((1-4a-aa)/(2-3a-aa)),
(-1,0), (-a,0), (a,0), (1,0).
a - корень уравнения aaa+9aa-a-1=0.
a = 0.3840429432601917.
Сверху вниз:
(0,2),
((a-4aa+aaa)/(-2+2a-8aa), (-1+2a-3aa)/(-1+a-4aa)),
((-a+4aa-aaa)/(-2+2a-8aa), (-1+2a-3aa)/(-1+a-4aa)),
(-(1+3a)/2, 1+a), ((-a+aa)/2, 1+a)),
((a-aa)/2, 1+a)), ((1+3a)/2, 1+a),
(-2a/(1+3a), (2+2a)/(1+3a)),
(2a/(1+3a), (2+2a)/(1+3a)),
(0, (2+2a)/(2+a-aa)),
(-(a+aa)/(2+4a), (1+3a)/(1+2a)),
((a+aa)/(2+4a), (1+3a)/(1+2a)),
(0, (2+6a)/(2+5a+aa)),
(-1/2,1), (-a/2,1), (a/2,1), (1/2,1), (0,2/3),
(-(1+3a)/(1-a), 0), (-1,0), (1,0), (1+3a)/(1-a), 0).
Опять используется: a - корень уравнения aaa+9aa-a-1=0.
a = 0.3840429432601917.
Сверху вниз:
(0,2), (-1/2,1), (-a,1), (a,1), (1/2,1),
(0, (2+6a)/(2+7a-aa)),
(-(a+aa)/(2+8a), (1+3a)/(1+4a)),
((a+aa)/(2+8a), (1+3a)/(1+4a)),
(0, 2/(2+a)),
(-2a/(3+a), (2+2a)/(3+a)),
(2a/(3+a), (2+2a)/(3+a)),
(-(1+3a)/(2+4a), (1+a)/(1+2a)),
(-(a-aa)/(2+4a), (1+a)/(1+2a)),
((a-aa)/(2+4a), (1+a)/(1+2a)),
((1+3a)/(2+4a), (1+a)/(1+2a)),
(-(2a+6aa)/(3+10a-aa), (2+8a-2aa)/(3+10a-aa)),
((2a+6aa)/(3+10a-aa), (2+8a-2aa)/(3+10a-aa)),
(0, 2/3),
(-(1+3a)/(1-a), 0), (-1,0), (1,0), ((1+3a)/(1-a), 0).
Отрезок, расположенный здесь на y=1, в принципе можно двигать вверх и вниз от 0 до 2, так что (0,2) и 4 точки внизу остаются на месте, а остальные пересчитываются и сдвигаются.
Здесь опять используется уже неоднократно встречавшееся значение
a=cos(2пи/7)/(1+cos(2пи/7)),
оно же корень уравнения aaa+9aa-a-1=0.
Численно a = 0.3840429432601917.
Сверху вниз:
(0,2),
(-(1+3a)/(2-2a), 1) = (-1.7469796037174672, 1),
(-1/2,1), (1/2,1),
((1+3a)/(2-2a) = (1.7469796037174672, 1),
(0,2/3),
(-(a+4aa-aaa)/(1+6a+aa), (4a+4aa)/(1+6a+aa)) =
= (-0.2657659627640713, 0.6159570567398215),
((a+4aa-aaa)/(1+6a+aa), (4a+4aa)/(1+6a+aa)) =
= (0.2657659627640713, 0.6159570567398215),
(-(1+a-aa)/(2+4a-2aa), (2-2aa)/(2+4a-2aa)) =
= (-0.7369762290995783, 0.5260475418008435),
(-(-a+4aa+aaa)/(2+4a-2aa)) =
= (-0.0810056738882147, 0.5260475418008435),
((-a+4aa+aaa)/(2+4a-2aa)) =
= (0.0810056738882147, 0.5260475418008435),
((1+a-aa)/(2+4a-2aa), (2-2aa)/(2+4a-2aa)) =
= (0.7369762290995783, 0.5260475418008435),
(-2a/(3-a), (2-2a)/(3-a)) =
= (-0.2936156327725145, 0.4709229114849903),
(2a/(3-a), (2-2a)/(3-a)) =
= (0.2936156327725145, 0.4709229114849903),
(0, 2a/(1+2a)) = (0, 0.4344166153783325),
(-4aa/(3+4a-3aa), (2-2aa)/(3+4a-3aa)) =
= (-0.1441129622465020, 0.4164985283102147),
(4aa/(3+4a-3aa), (2-2aa)/(3+4a-3aa)) =
= (0.1441129622465020, 0.4164985283102147),
(0, (2a-2aa)/(1+5a-2aa)) = (0, 0.1802153354993188),
(-1,0), (-a,0), (a,0), (1,0).
a - корень того же уравнения aaa-aa-9a+1=0.
a=0.1099162641747425. Сверху вниз:
(-1,2), (1,2), (1,1), (-a,1-a), (a,1-a), (0,2/(3+a)),
(-a,(2-2a)/(3-a)), (-(a+aa)/(3-a), (2-2a)/(3-a)),
((a+aa)/(3-a), (2-2a)/(3-a)), (a,(2-2a)/(3-a)),
(0, (2-2a)/(3+2a-aa)),
(-(1-5a-2aa)/(2+3a+aa), (1+2a+aa)/(2+3a+aa)),
(-(a+aa)/(2+3a+aa), (1+2a+aa)/(2+3a+aa)),
((a+aa)/(2+3a+aa), (1+2a+aa)/(2+3a+aa)),
((1-5a-2aa)/(2+3a+aa), (1+2a+aa)/(2+3a+aa)),
(0,(1-a)/2), (-a,(1-2a+aa)/2), (a,(1-2a+aa)/2),
(-1,0), (-a,0), (a,0), (1,0).
a - корень кубического уравнения aaa-aa-9a+1=0.
a=0.1099162641747425.
Сверху вниз: (0,1), (-1/4,3/4), (1/4,3/4),
(0,6a/(1+6a+aa)) = (0, 0.4003224353054432),
((-3a+aa)/(1+7a), 6a/(1+7a)) =
= (-0.1795324522488377, 0.3727209354318017)
((-a-aa)/(1+7a), 6a/(1+7a)) =
= (-0.0689481713723634, 0.3727209354318017),
((a+aa)/(1+7a), 6a/(1+7a)) =
= (-0.0689481713723634, 0.3727209354318017),
((3a-aa)/(1+7a), 6a/(1+7a)) =
= (0.1795324522488377, 0.3727209354318017),
(0, (3-3a)/(9-5a)) = (0, 0.3159904034189063),
((-1+4a+aa)/(1+10a-7aa), (6a-6aa)/(1+10a-7aa)) =
= (-0.2721411986980474, 0.2913782078956981),
((-a-4aa+aaa)/(1+10a-7aa), (6a-6aa)/(1+10a-7aa)) =
= (-0.0778890601009159, 0.2913782078956982),
((a+4aa-aaa)/(1+10a-7aa), (6a-6aa)/(1+10a-7aa)) =
= (0.0778890601009159, 0.2913782078956982),
((1-4a-aa)/(1+10a-7aa), (6a-6aa)/(1+10a-7aa)) =
= (0.2721411986980474, 0.2913782078956981),
(0, 3a/(1+4a)) = (0, 0.2290454929011846),
(-2a/(1+5a-4aa), (3a-3aa)/(1+5a-4aa) =
= (-0.1464325056212418, 0.1955057874744118),
(2a/(1+5a-4aa), (3a-3aa)/(1+5a-4aa) =
= (0.1464325056212418, 0.1955057874744118),
(-1,0), (-a,0), (a,0), (1,0),
((-3-2a+aa)/(8a-4aa), (-3+6a-3aa)/(8a-4aa)) =
= (-3.8600919128348545, -2.8600919128348545),
((3+2a-aa)/(8a-4aa), (-3+6a-3aa)/(8a-4aa)) =
= (3.8600919128348545, -2.8600919128348545).
a - корень кубического уравнения 8aaa-4aa-18a+1=0.
a=0.05495813208737119
В самом низу картинки должны быть точки (-1,0), (1,0), в самом верху (0,2), но все они не вошли в экран. Далее идем сверху вниз.
(-(-4aa+4a+3)/(-4aa+4a+7), 8/(-4aa+4a+7)) =
= (-0.4450418679126288, 1.1099162641747424),
((-4aa+4a+3)/(-4aa+4a+7), 8/(-4aa+4a+7)) =
= (0.4450418679126288, 1.1099162641747424),
(-0.5,1), (-a,1), (a,1), (0.5,1),
(-2a/(-2aa+3a+1), (2a+1)/(-2aa+3a+1) =
= (-0.0948507739368918, 0.9577874343941671)
(2a/(-2aa+3a+1), (2a+1)/(-2aa+3a+1) =
= (0.0948507739368918, 0.9577874343941671)
(0, 1/(a+1)) = (0, 0.9479049163983131),
((2a-1)/2/(-2aa+3a+2), 2/(-2aa+3a+2) =
= (-0.2061492220384588, 0.9264261944852804),
(-2a(-2aa+3a+1)/(-2aa+3a+2), 2/(-2aa+3a+2) =
= (-0.0590016110090197, 0.9264261944852804),
(2a(-2aa+3a+1)/(-2aa+3a+2), 2/(-2aa+3a+2) =
= (0.0590016110090197, 0.9264261944852804),
((-2a+1)/2/(-2aa+3a+2), 2/(-2aa+3a+2) =
= (0.2061492220384588, 0.9264261944852804),
(0, (-8aa+14a+1)/(-10aa+17a+1))
= (0, 0.9165826822144872),
(-(-4aa+8a+1)/(-4aa+9), 8/(-4aa+9)) =
(-0.1588336036970477, 0.8900837358252576),
((4aa+8a-1)/(-4aa+9), 8/(-4aa+9)) =
(-0.0609989246524371, 0.8900837358252576),
((-4aa-8a+1)/(-4aa+9), 8/(-4aa+9)) =
(0.0609989246524371, 0.8900837358252576),
((-4aa+8a+1)/(-4aa+9), 8/(-4aa+9)) =
(0.1588336036970477, 0.8900837358252576),
(0, (2a+1)/(-2aa+5a+1)) = (0, 0.8748109397138489).
Все необходимые тождества для наличия рядов из дубов доказаны аналитически.
На отрезке в основании фигуры разместим точки
(-1,0), (-a,0), (a,0), (1,0),
где a=cos(alfa)/(1+cos(alfa)), alfa=2пи/7.
Численно a=0.3840429432601917.
Вверху находится невошедшая в экран точка (0,1).
Из соображений наглядности картинка растянута по высоте в 10 раз.
На высотах h1=0.1 и h2=0.1216924061471810 расположены два горизонтальных отрезка с 4 дубами в каждом.
В принципе любая из этих высот h1, h2 может браться достаточно произвольно, а вторая вычисляется. Например, годятся 0.445041867912629 и 0.5. При этом число a всегда неизменно, оно также определяет пропорции на длинных боковых отрезках 1-го решения.
Координаты всех дубов выражаются аналитически по формулам для нахождения точки пересечения линий на плоскости. При h2=0.5 формулы проще, в частности, a*h1*h1+(a+1)*h1-(a+1)/2=0. Наверняка, можно также аналитически доказать принадлежность всех дубов указанным рядам. Но я ограничился численными значениями, полученными на 64-разрядах. В пределах этой точности отклонений дубов от указанных рядов нет.
Конечно, одни численные значения координат не являлись бы 100-процентным доказательством. Но есть еще общая теория, которая четко указывает конфигурацию дубов. Да и численные отклонения, если бы они были, то на таких несложных конструкциях обычно всплывают весомо, грубо, зримо, а не в квадриллионных дольках.
Координаты точек на 1-й горизонтали:
(-0.3456386489341625, 0.1),
(-0.0989246377572612, 0.1),
(0.0989246377572612, 0.1),
(0.3456386489341625, 0.1).
На 2-й горизонтали:
(-0.3373078334310038, 0.1216924061471810),
(-0.0370756169276120, 0.1216924061471810),
(0.0370756169276120, 0.1216924061471810),
(0.3373078334310038, 0.1216924061471810).
Точки на вертикальной осевой линии:
(0, 0.0909980507890740),
(0, 0.1109785087798926),
(0, 0.1346959966610240).
Самые верхние на рисунке:
(-0.0947096612998362, 0.1383471589857207),
(0.0947096612998362, 0.1383471589857207).
Чуть ниже:
(-0.1586139822121785, 0.1285812519974406),
(0.1586139822121785, 0.1285812519974406).
Еще ниже:
(-0.0973779487059027, 0.1140715212891486),
(0.0973779487059027, 0.1140715212891486).
Да вот беда: для полученных 120 дубов появляются, кроме всего прочего, 30 рядов по 6 дубов в каждом. Можно, конечно, было не заметить пару лишних дубов в таких рядах или сделать вид, что не заметили, тогда выйдет 360 рядов. Если 6-дубовые ряды вообще не учитывать, то оставшиеся 330 рядов ровно по 4 дуба в каждом - это тоже неплохо.
Но для математика остается факт, что далее обобщения задачи расползаются и теряют прежний простой четкий вид. Условие "4 дуба в каждом ряду" можно заменить на "не менее 4 дубов в каждом ряду". Понятно, что всего при 16 дубах такое уточнение было излишним и лишь наводило бы туман. Но далее надо либо переформулировать задачу, либо заведомо терять красивые комбинации.
На рисунке изображены далеко не все линии. По некоторым из тридцатки показан только один представитель.
Из точек самого внешнего хоровода на рисунке показаны все линии только для точки A, а для следующего хоровода только для точки B.
Пара внутренних хороводов подобна паре внешних, лишь повернута на 10 градусов.
Поэтому для доказательства законности достаточно установить, что именно через одну точку A на оси абсцисс проходят две наклонные линии, пересекающие точки 3-го (если считать снаружи) хоровода.
Для одной линии точка пересечения с осью абсцисс равна cos(2.5alfa)/cos(3.5alfa), для другой cos(alfa)/cos(3alfa), где alfa=пи/9. Или, что то же, cos(50 градусов)/cos(70 градусов) и cos(20 градусов)/cos(60 градусов). Или sin(40 градусов)/sin(20 градусов) и 2*cos(20 градусов), которые совпадают согласно формулам двойных углов.
Каждая точка внешнего хоровода состоит в 7 рядах. Но ряд соединяет пару таких точек. Так что внешний хоровод дает вклад 7*18/2=63 ряда. В следующем хороводе каждая точка тоже состоит в 7 рядах, но два из них учтены ранее. Поэтому вклад 2-го хоровода 5*18/2=45 рядов. И 3-й хоровод дает 18 рядов. Всего 126. На всякий случай на компьютере проверено наличие ровно 126 рядов, а также, что ни в один ряд не затесалось более 4 дубов.
Это размещение дает тот же коэффициент 126/72=7/4, как 60 дубов в 105 рядов. Однако, двумя хороводами 72 дуба в 126 рядов не разместить, поэтому на 72 дубах (и близких значениях) сильнейшим является размещение в 4 хоровода.
На одном рисунке показаны все ряды, на другом только нужные для сути дела, из них остальные получаются поворотами.
При четных K для упомянутой ранее вспомогательной задачи всегда можно закрыть наблюдателю обзор 3 точек, т.е. провести от него 3 луча, каждый из которых дважды пересекает окружность в исходных точках. 5 лучей получается при K=18 и K=24 (к ним мы вернемся позже). Зато 7 лучей получается при K = 30, 60, 90, 120, 150 и т.д. Это тоже, по-видимому, максимум. По крайней мере, компьютерный расчет не выявил ничего лучшего при K до 5000.
Рассмотрим рисунок. Он образован для K=30. Если радиус внутреннего круга принять за единицу, то радиус внешнего R=2cos(пи/10). Лучи из точки (R,0) образуют с осью абсцисс углы в 18, 30 и 36 градусов. Для проверки законности построения достаточно школьных знаний, учитывая, что косинус 72 градусов равен корню квадратному из пяти, минус 1, и всё поделить на 4.
Сравним с прежними результатами для 3 хороводов. Там 64 дуба (N=21) давали 84 ряда, 70 - 92, 76 - 100, а здесь из меньшего количества дубов мы получили даже больше рядов.
Более того, к имеющимся на картинке 60 дубам можно, уже без столь приятной симметрии, добавлять новые дубы. Понятно, что один добавленный дуб ничего нового не даст. А вот два можно разместить на любой линии, проходящей через пару из имеющихся 60 точек, и от 62 дубов мы будем иметь 106 рядов. Далее от каждого вновь добавленного дуба можно получить новый ряд из 4 дубов.
Новые точки можно получать так. На внешней окружности соединим отрезком пару точек, которые находятся на лучах под углом 0 и 12 градусов по отношению к оси абсцисс. Затем пару под углами 24 и 36 градусов. И т.д. Отрезки продлим за их концы. Полученные точки пересечения - искомые. Так можно добавить 15 дубов. Причем для 15-го мы сразу получим не 1, а два новых ряда.
Аналогично можно соединить точки на лучах под углами 12 и 24 градуса, и т.д. Это даст еще 15 рядов, так что для 90 дубов мы придем с 145 рядами. Далее можно соединять точки внутренней окружности. Кроме указанных 60 новых рядов (к 105 от 30 дубов), еще получатся 30 дополнительных, проходящих через центр рисунка. Так что для 120 дубов получим 195 рядов (что менее 210, которые можно получить просто удвоением всей рощи).
Но и при этом способе для 82 дубов получим 126 рядов, а это больше, чем 108, которое раньше получалось из трех полных хороводов.
Для 88 получим 132 ряда, что тоже больше прежних 116.
Для 94 получим 138 рядов, что больше прежних 124.
Для 100 получим 144 ряда, что больше прежних 132.
Для 106 получим 150 рядов, что больше прежних 140.
Для 112 получим 156 рядов, что больше прежних 148.
Для 118 получим 162 ряда, что больше прежних 156.
Далее для метода двух исходных хороводов идет новый всплеск количества рядов, и нарастание на количествах дубов, кратных 30, идет по крайней мере с коэффициентом 105/60=7/4. А по методу трех хороводов - с коэффициентом менее 4/3 по отношению к количеству дубов. Так что новый метод далее заведомо перекрывает старый.
Где же последний раз метод трех хороводов оказывается лучше?
По нему для 54 дубов (17-конечная звездочка плюс два дуба) можно получить 69 рядов, а исходя из двух хороводов можно получить 70 рядов (теряя при последовательном удалении 6 дубов соответственно 7, 6, 6, 6, 5, 5 рядов от исходных 105).
А последний раз три хоровода лучше на 53 дубах и дают 68 рядов (как и при 52 дубах), а два хоровода дают только 65 (105-7-6-6-6-5-5-5).
В связи с этим возникает вспомогательная задача. Окружность поделена точками на K равных частей. Требуется найти вне окружности точку, из которой было бы видно минимальное количество исходных точек. Другими словами, чтобы исходные точки максимально закрывали друг друга от взора наблюдателя, находящегося вне окружности. Сначала ограничимся случаем, когда K нечетно.
Чтобы две точки скрылись от обзора, это элементарно. Увы, возможно, это и есть максимум. По крайней мере, компьютерный расчет до K=5001 ничего нового не выявил. Это означает, что, как минимум, в пределах 15000 дубов, если их равномерно размешать на трех концентрических окружностях, - нет ничего лучше указанного достижения.
Однако, четное K дает нечто новенькое!
Доказательство законности аналогично. alfa=пи/N. Радиус среднего хоровода примем за 1. Дубы внешнего хоровода можно взять на расстоянии R=cos(2alfa)/cos(3alfa), а внутреннего - на r=sin(alfa/2)/cos(3alfa). Тогда на каждой из двух длинных вертикалей абсциссы точек по модулю одинаковы: cos(2alfa)/cos(3alfa)*sin(alfa/2) и sin(alfa/2).
Для 11-конечной звездочки и далее количество вариантов быстро растет, внутренний хоровод в них рассекается многими способами.
Теперь это можно доказать. Обозначим alfa=пи/N. Радиус среднего хоровода примем за 1. Тогда дубы внешнего хоровода можно взять на расстоянии R=cos(alfa)/cos(2alfa), а внутреннего - на r=sin(alfa/2)/cos(2alfa).
Соединим пару самых удаленных точек внешнего хоровода, например, самую верхнюю и самую нижнюю (см. рисунки для 7- и 9-конечной звездочек). Эта линия (пока только визуально) проходит через пару соседних точек внутреннего хоровода, оставляя остальные точки по одну сторону.
А точно от центра эта линия удалена на
R*sin(alfa/2)=cos(alfa)/cos(2alfa)*sin(alfa/2).
Абсциссы по модулю кандидатов из внутреннего хоровода:
r*cos(alfa)=sin(alfa/2)/cos(2alfa)*cos(alfa),
т.е. то же самое, и значит, 4 точки точно лежат на одной прямой.
Теперь соединим пару самых удаленных точек среднего хоровода, например, самую верхнюю и самую нижнюю. Она рассекает внутренний хоровод так, что по одну сторону остается ровно одна точка. Тогда от центра эта вертикаль удалена на sin(alfa/2). Абсциссы кандидатов по модулю:
r*cos(2alfa)=sin(alfa/2)/cos(2alfa)*cos(2alfa),
т.е. то же самое, и эти 4 точки тоже точно лежат на одной прямой.
Приравниваем по модулу ординаты четверного и пятерного углов, получаем уравнение
16aaaa+8aaa-12aa-4a+1=0.
Абсцисса самой верхней точки на рисунке:
(aa-bb)/(4aaa-4abb-3aa+bb).
Одна из точек во внутреннем хороводе:
(aa-bb,(aa-bb)b/a).
Точки внутреннего хоровода удалены от центра на (aa-bb)/a.
Крайние слева точки внутреннего хоровода имеют абсциссу (bb-aa)/a*SQRT((1+a)/2). Аналогично можно убедиться, что она совпадает с абсциссой самой верхней точки.
Следующими должны быть 34 дуба в 44 ряда. Точный расчет не произведен, но маловероятно, что он невозможен.
Начало координат (0,0) поместим в центральную точку на рисунке. Точка A пусть имеет координаты (1,0), точка B координаты (a,b). Тогда aa+bb=1. По формулам двойного угла точка C имеет координаты (aa-bb, 2ab). По формулам четверного угла точка E имеет координаты (aaaa-6aabb+bbbb, 4aaab-4abbb).
В силу симметрии относительно оси абсцисс точка D имеет ту же абсциссу, что и E, а ординату - отличающуюся знаком. В то же время координаты точки D можно вычислить по формулам тройного угла. Приравняв полученные двумя способами значения ординаты точки D, получим кубическое уравнение 8aaa+4aa-4a-1=0, откуда при надобности можно посмотреть на численные значения: a=0.6234898019, b=0.7818314824.
Точка H может быть вычислена как пересечение двух прямых, одна из которых проходит через A и B, другая - через начало координат. Это дает уравнение (1-x)b/(1-a)=2abx/(bb-aa), откуда x=(bb-aa)/(1+2a-4aa).
Далее вычисляем координаты точки из самого внутреннего хоровода, лежащей на пересечении линии AD и на вертикальной линии, проходящей через C. Вторая линия сразу дает x=aa-bb, а первая - уравнение
y=(1-x)(4abbb-4aaab)/(1-aaaa+6aabb-bbbb), откуда y=(bb-aa)b/a.
Тогда все точки внутреннего хоровода удалены от (0,0) на расстояние (bb-aa)/a.
По формуле половинного угла получаем абсциссу пары точек внутреннего хоровода, изображенных на вертикали, проходящей через H:
(bb-aa)/a*SQRT((1+a)/2). (SQRT - это квадратный корень.)
Осталось проверить, что ранее вычисленная абсцисса точки H имеет то же значение, и, значит, четыре точки точно лежат на одной вертикали, т.е.
(bb-aa)/(1+2a-4aa) = (bb-aa)/a*SQRT((1+a)/2).
Или, что то же, 2aa=(1+a)(1+2a-4aa)(1+2a-4aa).
Раскрыв скобки и понижая степень с помощью равенства 8aaa=1+4a-4aa, можно убедиться в справедливости тождества.
Наверняка, решение далеко не единственное. Топологические преобразования позволяют вчерне взглянуть на другие конфигурации, но точный расчет пока затруднителен.
Также используется a = 0.384042943260 - корень уравнения aaa+9aa-a-1=0.
4 точки на нижней горизонтальной линии:
(-1,0), (-a,0), (a,0), (1,0)
4 точки на короткой горизонтальной линии вверху:
((a-1)/2,1+a), (a(a-1)/2,1+a), (a(1-a)/2,1+a), ((1-a)/2,1+a).
Центральная точка: (0,2(1+a)/(3-a)).
Пара над ней:
((1-aa)/(aa-2a+5),4(1+a)/(aa-2a+5)) = (0.194664,1.264138),
((aa-1)/(aa-2a+5),4(1+a)/(aa-2a+5)).
На боковых сторонах треугольника:
(-4aa/(3aa+1),2(1-aa)/(3aa+1))=(-0.408990,1.182018),
(4aa/(3aa+1),2(1-aa)/3aa+1))=(0.408990,1.182018).
Ниже: (-0.403796,0.935864), (0.403796,0.935864).
По бокам: (-1.040830,0.742936), (1.040830,0.742936).
Законность еще двух точек на центральной вертикали вытекает из симметрии.
Без дуба точка вверху картинки на пересечении двух линий: (0,2).
Не вошли в экран снизу: (0,2(1+a)/(1-3a))=(0,-18.195669)
и сверху: (2a/(a-1),(2(1+a)/(1-a))=(-1.246980,4.493959),
(2a/(1-a),2(1+a)/1-a))=(1.246980,4.493959).
(0,2), (-1,0), (1,0), (-a,0), (a,0), (0,2a),
((a+1)/2,1-a), (-(a+1)/2,1-a), ((1-a)/2,1+a), ((a-1)/2,1+a),
(-2a/(a+3),2(a+1)/(a+3)), (2a/(a+3),2(a+1)/a+3),
(-a(a+1)/(3a+1),4a/(3a+1)), (a(a+1)/(3a+1),4a/(3a+1),
((aa-2a+1)/(aa-4a-1),-4a(a+1)/(aa-4a-1)),
(-(aa-2a+1)/(aa-4a-1),-4a(a+1)/(aa-4a-1)),
(a(aa-2a+1)/(aa-4a-1),-4a(a+1)/(aa-4a-1)),
(-a(aa-2a+1)/aa-4a-1),-4a(a+1)/(aa-4a-1)),
(0,(6aa+2)/(aa+3)), (0,2(a+1)(-5aa+2a-1)/(aaa-9aa+3a-3)),
((aa-2a+1)/(aa-2a-3),-8a/(aa-2a-3),
(-(aa-2a+1)/(aa-2a-3),-8a/(aa-2a-3),
где a - корень кубического уравнения aaa+9aa-a-1=0,
a = 0.384042943260.