Высший математический юмор

Трудно, друзья, считать высшую математику не трудной наукой. Даже если взять простую арифметику, или геометрию с алгеброй, то и эти поднауки тоже будут многим не по зубам.
Правда многие раскусывают и грызут математические орехи с лёгкостью и удовольствием. Для некоторых математика может казаться изысканно-утончённой и недосягаемо сложной вычурности. Иногда даже считают её подозрительно высшей и дают ей разные оттенки. Для меня, так математика скорее комична и юмористична, чем сложна. Самая обычная алгебра и в особенности геометрия, в которых демонстрируются не только значки, циферки, буквочки, любопытные и занимательные чёрточки, штришки, пунктирчики и модельки с их красивостью и кристально ясной логикой, характеризующей абстрактность, точность и экстравагантность изложения, моделирования и пояснения, могут рассказать о юмористичности изобретателей головоломок и законов и комиков, умеющих разгадывать математические головоломки.

Каждый раз, когда я вдумчиво всматриваюсь в формулы, формулировки и условия задачек, пытаясь зазубрить на зубок теоремы, я ищу смысл фантазии в фантастических многогранниках, с правильными, полуправильными и вырожденными сверх многоугольными моделями живописных фракталов, которые являют примеры фантастики и фантасмагории математики,  вычерченных на полях высшей геометрии Природы. Фантазия самого гениального художника блекнет на фоне фантастических картин, которые рисует мороз на запотевших окошках веранды. Для меня математика всегда была достаточно трудным предметом, хотя я пытался изо всех сил понять и познать в том объёме, который необходим для моей профессиональной деятельности и даже немного глубже.

М.В. Ломоносов утверждал, что в природе всё математически точно и определённо, и если есть какие-то сомнения, то наше невежество ничего не отнимает от этой достоверности. Если бы весь мир математиков сомневался в том, что дважды два не пять и не три, а всё-таки у всех сомневающихся это будет равно четвёрке, то это общей картины не портит. Профессиональные математики при изучении пространственных форм и количественных отношений получают огромное удовольствие при составлении головоломных задач и удовлетворения своего математического тщеславия при решении и изобретении новых вариантов, даже если при этом относиться к математике серьёзно не могут из-за занимательности занятий, уроков связанных с математическими историями. Особенно много занимательного в юмористических инцидентах, связанных с историями решения задачек по геометрии.

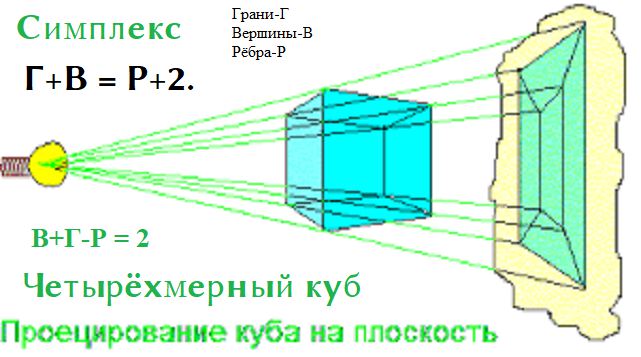
Узоры геометрии, кристаллографии, так же как узоры графика, художника, зодчего или узоры рифмоплетения поэтов, вариаций музыкантов, должны гармонически соответствовать друг другу. Особенность математики в красоте и универсальности геометрических законов, которые действуют в кристаллах неживой и живой материи и поэтому все выдающиеся гениальные и не очень математики преуспели в любом творчестве и даже в юморе, прибауточных шутках, которые в связи с математическим уклоном могут стать плоскими или объёмными. Трёх мерный юмор пытается возвысить, расширить и углубить в математике творческие возможности, создавая анекдотические завитки, сферу шуток и приколов и подмножество в подпространстве на подинформационном поле. Но это "под" существует в пространстве трех измерений, а что будет в четвертом или "над"? Шлефли установил, что там, где над пространством имеют вид на жительство шесть правильных гипертел - аналогов платоновых шуточек, названных ячейками политопа. Итак, политоп - крайний член последовательности все усложняющихся геометрических образцов: точка - линия - многоугольник - многогранник - политоп. Другой аналог Платоновых шуточек-гиперкуб, или "тессаракт", или "измерительный политоп". Шутки шутками, но то, как куб можно получить, перемещая квадрат по третьему измерению, так и сверх-куб образуется от движения обычного куба вдоль четвертого измерения. Но об этом ниже.

Известна история о Фредерике Содди, которому Нобелевский комитет не дал вторую премию за упаковочные головоломки по причине их юмористичной ироничности. Вопрос об упаковках - не праздный и не абстрактный. Он связан со строением вещества, его прочностью, а потому кровно интересует специалистов в разных областях науки. К примеру, каково максимальное число сфер может одновременно поцеловать одну такую же, целуясь при этом со своими соседями? На плоскости задача проста и красива, шесть кругов касаются седьмого в центре, Но в трёхмерном пространстве дело обстоит сложнее. Не даром выдающийся математик Ньютон так и не смог доказать астроному Дэвиду Грегори, что таких целующихся сфер может быть не больше тринадцати, включая и расцелованную ими со всех сторон. Составив правильный двадцатигранник (икосаэдр), Хоппе придумал такое расположение чёртовой дюжины шаров, в которое всё-таки смог втиснуть четырнадцатый. Для того, чтобы найти вариант расположения шаров, нужно представить сверх мерную  спаренную сферу-гиперсферу и те, кто смог это представить, смогут без труда иметь представление четырёх мерного пространства. И вот, только Бернгард Риман сумел это сделать, назвав своё представление «О гипотезах, образующих основания геометрии», которую все, кто тоже стал представлять представление назвали «римановой». Представляете, если изобразить куб в трёх мерном пространстве на плоском картоне, мы получим два квадрата один в другом, соединённые вершинами-какая красота! Я не представляю, как это может быть.

Математическая красота это одно из самых загадочных явлений природы. И как в законах строения и развития природных тел мы имеем разные уровни, так есть они и в прекрасной математике. И на самом высшем уровне, может быть, находятся абстрактнейшие математические теории и высшие музыкальные творения гениальных композиторов и нанизу есть непотребное, хотя и не уродливое. Не всем дано подняться на эти вершины, где, как в капле воды отражается солнце, так некоторый намек на высшую красоту мы можем постичь, внимательно рассматривая такое скромное явление, как ледяные узоры на стеклах, кристаллические решётки в микроскопе или, пробуя разрешить головоломные задачи, построить голограммы. Одним из таких красот являются звездчатые, колючие многогранники, названные телами Кеплера-Пуансо. Два тетраэдра, прошедших один сквозь другой, образуют восьмигранник. Иоганн Кеплер присвоил этой фигуре имя «стелла октангула» -«восьмиугольная звезда». Она встречается и в природе: это так называемый двойной кристалл. Мы вынуждены признать «стеллу октангулу» правильным многогранником: ведь все ее грани - правильные треугольники одинакового размера и все углы между ними равны! Икосаэдр и додекаэдр дарят миру сразу четыре «почти правильных многогранника». Один из них-малый звездчатый додекаэдр, полученный впервые Иоганном Кеплером.

Столетиями математики не признавали за всякого рода звездами права называться многоугольниками из-за того, что стороны их пересекаются. А тут - геометрическое тело, гранями которого служат пятиконечные звезды, да еще вдобавок пересекающиеся! Какой же это многогранник?! Людвиг Шлефли не изгонял геометрическое тело из семейства многогранников только за то, что его грани само пересекаются, тем не менее, оставался непреклонным, как только речь заходила про малый звездчатый додекаэдр. Довод его был прост и весом: это кеплеровское создание не подчиняется формуле Эйлера! Его колючки образованы двенадцатью гранями, тридцатью ребрами и двенадцатью вершинами, и, следовательно, В+Г—Р вовсе не равняется двойке.

В современной математике юмористы употребляют термин "наглядная геометрия", относя к ней те геометрические вопросы и теоремы, которые имеют "наглядный" геометрический смысл. Теория выпуклых и впуклых фигур, и, в частности, выпуклых и вогнутых звездчатых многогранников, относится к наглядной геометрии. Ее теоремы имеют обычно элементарную формулировку и яркий геометрический смысл, хотя доказательства часто бывают весьма сложными. Вопросами этой теории занимались математики разных эпох, однако содержание этой теории не только не исчерпано, но, наоборот, в последние десятилетия она послужила темой для выдающихся работ юмористических геометров. Так в изображении куба в трёхмерном пространстве на плоском картоне можно получить два квадрата один в другом, соединённые вершинами. Если спроецировать четырёхмерный куб, получим по аналогии два куба один в другом, и тут тоже вершины попарно соединены, то же самое и с четырёхмерной сферой.

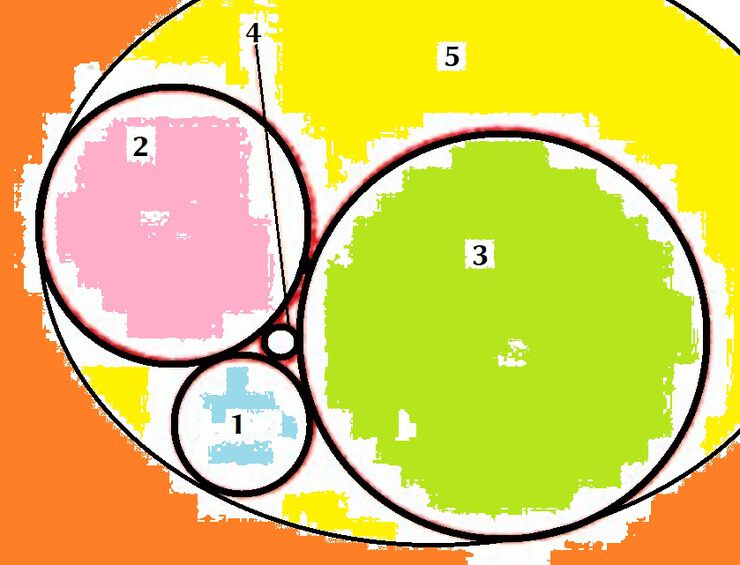
Проецируя глобус, геометр с юмором пропускает одну её полусферу сквозь другую, соединяя их проекции(круги только по границе окружности как квадраты по вершинам). Вычерчиваются два шара, прошедшие один через другой и соединённые только по внешним поверхностям. Конечно, вообразив такое, изобразить гиперсферу невозможно без иронического подхода к процессу, иначе получается мистика, похожая на четырёх мерного симплекса-самой простейшей из всех мистических фигур.

Идея четырёхмерного пространства всегда увлекала высших математиков с эзотерическим мышлением и служила пищей для математических "притчей во языцах", начиная с Платона. Неоплатоники с эзотерическим складом ума развили представления о реальном мире, четырёх мерном виртуальном и даже семи мерном астрально потустороннем. Вот и в самой Библии во Втором Послании Апостола Павла к Коринфянам упоминается третий небосвод и вознесение в духе. Сам пророк Иоанн, увидел « город четырёх-квадратный», я уже не говорю о материалистах ленинцах, которые склонились перед n-мерностью окружающего КПСС пространства. Нет слов.

Цитируя определения Гельмгольца, что геометрия-это интуиция математическо-философский мудрец Ганс Райхенбах набабахал: « Пользуясь нашей геометрической интуицией, мы математики с философской мудростью ограничены своим личным опытом, который усложняет представление о положении точки на прямой или в объёме пересечения линий в точках, расположения сферы в объёме. Наша интуиция имеет вообразительную функцию, связанную с нашим чувственным функционалом в виде опыта, так к примеру начертанный на стене треугольник как часть орнамента в виде трёх букв треуголки, но вместе с тем у творчески развитой интуиции имеется и нормативная функция, которая не позволяет взглянуть на изображённый орнамент без иронии». Чтобы развить умение обозревать и усовершенствовать не только глазомер, но и интуитивно-пространственное видение  художник старается видеть невозможные вещи, изображая их на двумерной плоской картине в перспективе трёх мерности, подчёркивая формы с помощью света, тени и светотеневого пятна. Многие же графики знают, что означает обман зрения, когда нарушаются элементарные правила графики и законы аксонометрии.

Вот математики А.Н. Коркин и Е.Золотарёв взяли и доказали, сколько целующихся может быть в четырёхмерном пространстве. У них получилось 24, а в семи мерном 126. Кроме того, в четырёх мерный куб впишется обычный трёхмерный, объём которого больше объёма одной гиперповерхности гиперкуба. А по их новым доказательствам в V-мерный куб с ребром в один миллиметр, поместится авианосец и может даже впихнуть весь 3D-мир, если он достигнет определённой величины. Мне на факультативных занятиях по математике, профессор политеха предложил изготовить фигурку в виде ёлочной игрушки из листов Мёбиуса. Я долго пыжился и всё-таки придумал. Потом это мне пригодилось в моей профессиональной деятельности инженера электронной техники.

Скажите, а вы когда-нибудь пробовали стать между двух параллельных зеркал и посмотреть на себя одновременно спереди и сзади? Вы конечно же увидели бесконечный коридор с множественностью изображений, в которых трудно понять где левая, а где правая сторона. Это-то и навело меня на мысль о том, что одновременно есть и мир, и антимир, рациональность не может существовать без иррациональности. Правда в математике не бывает без присутствия лжи и добро только тогда себя обнаруживает, если рядом есть зло. Каждый дурак, который хоть разочек вникал в гармонию окружающего мира, ища адекватный смысл и какие-то закономерности, понимал, что это и есть истинная красота математического юмора, не существующего без уродства.

«Живые источники математического творчества неотделимы от познания мироздания и задач управления, изменения и контроля», -утверждает академик А.Н. Колмогоров. «Числа не управляют миром, но показывают, как управляется мир», -так иносказательно переработав пифагорейскую мудрость И.В. Гёте высказывал мысль о том, что в первооснове вещей лежат некие простые математические соотношения, пропорции и уравнения, по которым строятся фигуры. Числа описывают закон движения, изменения и трансформации, фигуры наглядно показывают как это происходит. Геометрические модели стали символами структурного порядка, в котором наглядно видно ветви древа, спрятанные под листвой непонятных формул и абстрактных идей.

Огонь-тетраэдр, Земля-куб, воздух-октаэдр, вода-инкасаэдр и Вселенная долдекаэдр, создают общую модель и узор устойчивого равновесия геометрической мозаики правильных и не очень многоугольников в симметрии гексагональности. Такое можно видеть, если понаблюдать за пчёлами, строящими свой дом, это видно под микроскопом в кристаллах у минералов, об этом много говорят кристаллографы и теоретики кристаллоскопии. А если отлететь на звездолёте недалеко от планеты Земля, то можно многое увидеть невооружённым оком.

Кристаллологи и кристаллографы предложили совместную гипотезу, которую назвали додекаэдро-икосаэдровой по форме, грани которого сохранились на земле. Мозаика, покрывшая глобус в результате этой работы, состояла ровно из двадцати правильных треугольников. Иными словами, она представляла собою икосаэдр. Можно подумать, что язык математики очень замысловатый и без словаря не обойтись. На самом деле, математический язык - предельно точный, четкий, способный рассказать о самых главных, существенных свойствах Природы. Именно потому, что он лишен всяческих излишеств, язык этот может служить скелетом мысли, какой бы сложной или непривычной она ни была.

Можно преуспеть в доходчивости изложения, уйдя от разъяснения сущности проблемы и ограничившись лишь смутными намеками на нее и таким образом обмануть познающего, внушив ему иллюзию понимания. Можно, наоборот, квалифицированно и точно изложить проблему, но так, что неподготовленный опознаватель скоро потеряет мысль трактователя, и лишится возможности следовать за ней дальше. А можно преподнести всё с юмором в виде шутки, применив по мере возможности рифмоплётки. Все, чем богат мир, доступно нашему глазу, но умеем ли мы видеть всю красоту и мудрость обозреваемого мира? Боюсь, что нет. Мир сияет вокруг нас тысячами красок, он готов раскрыть нам тысячи тайн. А мы - слепы. Мы видим лишь малую долю этих сокровищ. Да и чему удивляться, ведь это только говорят, что человек венец творения, венец природы... А давно ли венец спрыгнул с древа и перестал бегать на четвереньках, ведя счёт на пальцах, разгоняя обезьян и пугая попугаев?! Вон он идёт-зодчий, ваятель, создатель математики, вон он берёт в руки инструмент и начинает отбивать от валуна лишнее, создавая гармонию кристалла Вселенского мироздания. Говорят, у него это получается.